V tejto téme budeme podrobne hovoriť o výpočte neurčitých integrálov pomocou takzvaného „vzorca integrácie podľa častí“. Budeme potrebovať tabuľku neurčitých integrálov a tabuľku derivácií. V prvej časti budú analyzované štandardné príklady, ktoré sa väčšinou nachádzajú v štandardných výpočtoch a testoch. Zložitejšie príklady sú uvedené v druhej časti.

Vyhlásenie problému v štandardnom prípade je nasledovné. Povedzme, že pod integrálom máme dve funkcie rôzneho charakteru: polynomiálna a goniometrická funkcia, polynóm a logaritmus, polynóm a inverzná goniometrická funkcia atď. V tejto situácii je výhodné oddeliť jednu funkciu od druhej. Zhruba povedané, má zmysel rozdeliť integrand na časti - a zaoberať sa každou časťou samostatne. Odtiaľ pochádza názov: „integrácia po častiach“. Aplikácia tejto metódy je založená na nasledujúcej vete:

Nech sú funkcie $u(x)$ a $v(x)$ diferencovateľné na nejakom intervale a na tomto intervale existuje integrál $\int v \; du$. Potom na rovnakom intervale existuje aj integrál $\int u \; dv$ a platí nasledujúca rovnosť:

\begin(rovnica) \int u \; dv=u\cdot v-\int v\; du \end(rovnica)

Vzorec (1) sa nazýva „vzorec integrácie podľa častí“. Niekedy pri aplikácii vyššie uvedenej vety hovoria o použití „metódy integrácie podľa častí“. Pre nás bude dôležitá podstata tejto metódy, ktorú zvážime na príkladoch. Existuje niekoľko štandardných prípadov, v ktorých jasne platí vzorec (1). Práve tieto prípady sa stanú témou tejto stránky. Nech $P_n(x)$ je polynóm n-tého stupňa. Predstavme si dve pravidlá:

Pravidlo č.1

Pre integrály v tvare $\int P_n(x) \ln x \;dx$, $\int P_n(x) \arcsin x \;dx$, $\int P_n(x) \arccos x \;dx$, $\ int P_n(x)\arctg x \;dx$, $\int P_n(x) \arcctg x \;dx$ vezmeme $dv=P_n(x)dx$.

Pravidlo č. 2

Pre integrály v tvare $\int P_n(x) a^x \;dx$ ($a$ je nejaké kladné číslo), $\int P_n(x) \sin x \;dx$, $\int P_n(x ) \ cos x \;dx$, $\int P_n(x)ch x \;dx$, $\int P_n(x) sh x \;dx$ vezmeme $u=P_n(x)$.

Dovoľte mi okamžite poznamenať, že vyššie uvedené záznamy by sa nemali brať doslovne. Napríklad v integráloch v tvare $\int P_n(x) \ln x \;dx$ nebude nevyhnutne presne $\ln x$. Môžu sa tam nachádzať $\ln 5x$ aj $\ln (10x^2+14x-5)$. Tie. zápis $\ln x$ treba brať ako akési zovšeobecnenie.

Ešte jedna vec. Stáva sa, že vzorec integrácie podľa častí sa musí použiť niekoľkokrát. Povedzme si o tom podrobnejšie v príkladoch č.4 a č.5. Teraz prejdime priamo k riešeniu typických problémov. Riešením problémov, ktorých úroveň je mierne vyššia ako štandard, sa zaoberá druhá časť.

Príklad č.1

Nájdite $\int (3x+4) \cos (2x-1) \; dx$.

Pod integrálom je polynóm $3x+4$ a goniometrická funkcia $\cos (2x-1)$. Toto je klasický prípad použitia vzorca, takže zoberme daný integrál po častiach. Vzorec vyžaduje, aby integrál $\int (3x+4) \cos (2x-1)\; dx$ bol zastúpený v tvare $\int u\; dv$. Musíme zvoliť výrazy pre $u$ a pre $dv$. Môžeme brať $3x+4$ ako $u$, potom $dv=\cos (2x-1)dx$. Môžeme vziať $u=\cos (2x-1)$, potom $dv=(3x+4)dx$. Aby sme urobili správnu voľbu, obráťme sa na. Daný integrál $\int (3x+4) \cos (2x-1)\; dx$ spadá pod tvar $\int P_n(x) \cos x \;dx$ (polynóm $P_n(x)$ v našom integráli má tvar $3x+4$). Podľa treba zvoliť $u=P_n(x)$, t.j. v našom prípade $u=3x+4$. Pretože $u=3x+4$, potom $dv=\cos(2x-1)dx$.

Jednoduchý výber $u$ a $dv$ však nestačí. Budeme tiež potrebovať hodnoty $du$ a $v$. Keďže $u=3x+4$, potom:

$$ du=d(3x+4)=(3x+4)"dx=3dx.$$

Teraz sa pozrime na funkciu $v$. Keďže $dv=\cos(2x-1)dx$, potom podľa definície neurčitého integrálu máme: $ v=\int \cos(2x-1)\; dx$. Aby sme našli požadovaný integrál, použijeme na diferenciálne znamienko nasledovné:

$$ v=\int \cos(2x-1)\; dx=\frac(1)(2)\cdot \int \cos(2x-1)d(2x-1)=\frac(1)(2)\cdot \sin(2x-1)+C=\frac (\sin(2x-1))(2)+C. $$

Nepotrebujeme však celú nekonečnú množinu funkcií $v$, ktorá je popísaná vzorcom $\frac(\sin(2x-1))(2)+C$. Potrebujeme nejaké jeden funkcie z tejto sady. Ak chcete získať požadovanú funkciu, musíte namiesto $C$ nahradiť nejaké číslo. Najjednoduchším spôsobom je samozrejme nahradiť $C=0$, čím získame $v=\frac(\sin(2x-1))(2)$.

Poďme si teda dať všetko vyššie uvedené dokopy. Máme: $u=3x+4$, $du=3dx$, $dv=\cos(2x-1)dx$, $v=\frac(\sin(2x-1))(2)$. Nahradením tohto všetkého do pravej strany vzorca máme:

$$ \int (3x+4) \cos (2x-1) \; dx=(3x+4)\cdot\frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2)\cdot 3dx. $$

V skutočnosti zostáva len nájsť $\int\frac(\sin(2x-1))(2)\cdot 3dx$. Ak vezmeme konštantu (t.j. $\frac(3)(2)$) mimo znamienka integrálu a použijeme metódu jej zavedenia pod znamienko diferenciálu, dostaneme:

$$ (3x+4)\cdot \frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2)\cdot 3dx= \frac((3x+ 4) )\cdot\sin(2x-1))(2)-\frac(3)(2)\int \sin(2x-1) \;dx= \\ =\frac((3x+4)\cdot \ sin(2x-1))(2)-\frac(3)(4)\int \sin(2x-1) \;d(2x-1)= \frac((3x+4)\cdot\sin ( 2x-1))(2)-\frac(3)(4)\cdot (-\cos (2x-1))+C=\\ =\frac((3x+4)\cdot\sin(2x - 1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C. $$

Takže $\int (3x+4) \cos (2x-1) \; dx=\frac((3x+4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C$. V skrátenej forme je proces riešenia napísaný takto:

$$ \int (3x+4) \cos (2x-1) \; dx=\left | \začiatok(zarovnané) & u=3x+4; \; du=3xdx.\\ & dv=\cos(2x-1)dx; \; v=\frac(\sin(2x-1))(2). \end(zarovnané) \right |=\\ =(3x+4)\cdot\frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2) \cdot 3dx= \frac((3x+4)\cdot\sin(2x-1))(2)-\frac(3)(2)\int \sin(2x-1) \;dx=\\ = \frac((3x+4)\cdot\sin(2x-1))(2)-\frac(3)(4)\cdot (-\cos (2x-1))+C= \frac((3x +4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot\cos (2x-1)+C. $$

Neurčitý integrál bol nájdený po častiach, zostáva už len zapísať odpoveď.

Odpoveď: $\int (3x+4) \cos (2x-1) \; dx=\frac((3x+4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C$.

Verím, že tu je otázka, tak sa ju pokúsim sformulovať a dať odpoveď.

Prečo sme vzali presne $u=3x+4$ a $dv=\cos(2x-1)dx$? Áno, integrál je vyriešený. Ale možno keby sme zobrali $u=\cos (2x-1)$ a $dv=(3x+4)dx$ integrál by sa tiež našiel!

Nie, ak zoberieme $u=\cos (2x-1)$ a $dv=(3x+4)dx$, tak z toho nič dobré nebude – integrál sa nezjednoduší. Posúďte sami: ak $u=\cos(2x-1)$, potom $du=(\cos(2x-1))"dx=-2\sin(2x-1)dx$. Navyše, keďže $ dv =(3x+4)dx$, potom:

$$ v=\int (3x+4) \; dx=\frac(3x^2)(2)+4x+C.$$

Ak vezmeme $C=0$, dostaneme $v=\frac(3x^2)(2)+4x$. Nahraďte teraz nájdené hodnoty $u$, $du$, $v$ a $dv$ do vzorca:

$$ \int (3x+4) \cos (2x-1) \; dx=\cos (2x-1)\cdot \left(\frac(3x^2)(2)+4x \right) - \int \left(\frac(3x^2)(2)+4x \right) \cdot (-2\sin(2x-1)dx)=\\ =\cos (2x-1)\cdot \left(\frac(3x^2)(2)+4x \right) +2\cdot\ int \left(\frac(3x^2)(2)+4x \right) \sin(2x-1)\;dx $$

A k čomu sme dospeli? Dostali sme sa k integrálu $\int \left(\frac(3x^2)(2)+4x \right) \sin(2x-1)\;dx$, ktorý je zjavne zložitejší ako pôvodný integrál $\int (3x+4) \cos (2x-1) \; dx$. To naznačuje, že výber $u$ a $dv$ bol urobený zle. Po použití vzorca integrácie podľa častí by mal byť výsledný integrál jednoduchší ako pôvodný. Pri hľadaní neurčitého integrálu po častiach ho musíme zjednodušiť, nie komplikovať, takže ak sa po aplikovaní vzorca (1) integrál skomplikuje, výber $u$ a $dv$ bol urobený nesprávne.

Príklad č.2

Nájsť $\int (3x^4+4x-1) \ln 5x \; dx$.

Pod integrálom je polynóm (t.j. $3x^4+4x-1$) a $\ln 5x$. Tento prípad spadá pod , takže zoberme integrál po častiach. Daný integrál má rovnakú štruktúru ako integrál $\int P_n(x) \ln x\; dx$. Opäť, ako v príklade č. 1, musíme vybrať časť integrandu $(3x^4+4x-1) \ln 5x \; dx$ ako $u$ a niektorú časť ako $dv$. Podľa , treba zvoliť $dv=P_n(x)dx$, t.j. v našom prípade $dv=(3x^4+4x-1)dx$. Ak z výrazu $(3x^4+4x-1) \ln 5x \; dx$ "odstráni" $dv=(3x^4+4x-1)dx$, potom zostane $\ln 5x$ - to bude funkcia $u$. Takže $dv=(3x^4+4x-1)dx$, $u=\ln 5x$. Na použitie vzorca potrebujeme aj $du$ a $v$. Keďže $u=\ln 5x$, potom:

$$ du=d(\ln 5x)=(\ln 5x)"dx=\frac(1)(5x)\cdot 5 dx=\frac(1)(x)dx. $$

Teraz nájdime funkciu $v$. Pretože $dv=(3x^4+4x-1)dx$, potom:

$$ v=\int(3x^4+4x-1)\; dx=\frac(3x^5)(5)+2x^2-x+C. $$

Z celej nájdenej nekonečnej množiny funkcií $\frac(3x^5)(5)+2x^2-x+C$ si musíme jednu vybrať. A najjednoduchšie to urobíte tak, že vezmete $C=0$, t.j. $v=\frac(3x^5)(5)+2x^2-x$. Všetko je pripravené na aplikáciu vzorca. Dosaďte hodnoty $u=\ln 5x$, $du=\frac(1)(x)dx$, $v=\frac(3x^5)(5)+2x^2-x$ a $dv=(3x^4+4x-1)dx$ budeme mať:

$$ \int (3x^4+4x-1) \ln 5x \; dx=\left | \začiatok(zarovnané) & u=\ln 5x; \; du=\frac(1)(x)dx.\\ & dv=(3x^4+4x-1)dx; \; v=\frac(3x^5)(5)+2x^2-x. \end(zarovnané) \right |=\\ =\ln 5x \cdot \left (\frac(3x^5)(5)+2x^2-x \right)-\int \left (\frac(3x^ 5)(5)+2x^2-x \vpravo)\cdot \frac(1)(x)dx=\\ =\vľavo (\frac(3x^5)(5)+2x^2-x \vpravo )\cdot\ln 5x -\int \left (\frac(3x^4)(5)+2x-1 \right)dx=\\ =\left (\frac(3x^5)(5)+2x^ 2-x \vpravo)\cdot\ln 5x - \vľavo (\frac(3x^5)(25)+x^2-x \vpravo)+C=\\ =\vľavo (\frac(3x^5) (5)+2x^2-x \vpravo)\cdot\ln 5x - \frac(3x^5)(25)-x^2+x+C. $$

Odpoveď: $\int (3x^4+4x-1) \ln 5x \; dx=\left (\frac(3x^5)(5)+2x^2-x \right)\cdot\ln 5x - \frac(3x^5)(25)-x^2+x+C$.

Príklad č.3

Nájdite $\int \arccos x\; dx$.

Tento integrál má štruktúru $\int P_n(x) \arccos x \;dx$, spadajúcu pod . Chápem, že hneď vyvstane rozumná otázka: "kde v danom integráli $\int\arccos x \; dx$ skryli polynóm $P_n(x)$? Polynóm tam nie je, iba arkozínus a hotovo! “ V skutočnosti sa však pod integrálom nenachádza len arckosínus. Uvediem integrál $\int arccos x\; dx$ v tomto tvare: $\int 1\cdot\arccos x \; dx$. Súhlaste s tým, že vynásobením jedným sa integrand nezmení. Táto jednotka je $P_n(x)$. Tie. $dv=1\cdot dx=dx$. A ako $u$ (podľa ) berieme $\arccos x$, t.j. $u=\arccos x$. Hodnoty $du$ a $v$, ktoré sú zahrnuté vo vzorci, nájdeme rovnakým spôsobom ako v predchádzajúcich príkladoch:

$$ du=(\arccos x)"dx=-\frac(1)(\sqrt(1-x^2))dx;\\ v=\int 1\; dx=x+C. $$

Rovnako ako v predchádzajúcich príkladoch, za predpokladu $C=0$ dostaneme $v=x$. Nahradením všetkých nájdených parametrov do vzorca dostaneme nasledovné:

$$ \int \arccos x \; dx=\left | \begin(zarovnané) & u=\arccos x; \; du=-\frac(1)(\sqrt(1-x^2))dx.\\ & dv=dx; \; v=x. \end(zarovnané) \right |=\\ =\arccos x \cdot x-\int x\cdot \left(-\frac(1)(\sqrt(1-x^2))dx \right)= \ arccos x \cdot x+\int \frac(xdx)(\sqrt(1-x^2))=\\ =x\cdot\arccos x-\frac(1)(2)\cdot\int (1-x ^2)^(-\frac(1)(2))d(1-x^2)= =x\cdot\arccos x-\frac(1)(2)\cdot\frac((1-x^ 2)^(\frac(1)(2)))(\frac(1)(2))+C=\\ =x\cdot\arccos x-\sqrt(1-x^2)+C. $$

Odpoveď: $\int\arccos x\; dx=x\cdot\arccos x-\sqrt(1-x^2)+C$.

Príklad č.4

Nájdite $\int (3x^2+x) e^(7x) \; dx$.

V tomto príklade bude potrebné použiť vzorec integrácie podľa častí dvakrát. Integrál $\int (3x^2+x) e^(7x) \; dx$ má štruktúru $\int P_n(x) a^x \;dx$. V našom prípade $P_n(x)=3x^2+x$, $a=e$. Podľa máme: $u=3x^2+x$. Podľa toho $dv=e^(7x)dx$.

$$ du=(3x^2+x)"=(6x+1)dx;\\ v=\int e^(7x)\;dx=\frac(1)(7)\cdot \int e^( 7x)\;d(7x)=\frac(1)(7)\cdot e^(7x)+C=\frac(e^(7x))(7)+C. $$

Opäť, ako v predchádzajúcich príkladoch, za predpokladu $C=0$, máme: $v=\frac(e^(7x))(7)$.

$$ \int (3x^2+x) e^(7x) \; dx=\left | \begin(zarovnané) & u=3x^2+x; \; du=(6x+1)dx.\\ & dv=e^(7x)dx; \; v=\frac(e^(7x))(7). \end(zarovnané) \right |=\\ =(3x^2+x)\cdot\frac(e^(7x))(7)-\int \frac(e^(7x))(7)\cdot (6x+1)dx= \frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \int (6x+1) e^(7x)\ ;dx. $$

Dospeli sme k integrálu $\int (6x+1) e^(7x)\;dx$, ktorý opäť musíme brať po častiach. Ak vezmeme $u=6x+1$ a $dv=e^(7x)dx$, máme:

$$ \frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \int (6x+1) e^(7x)\;dx=\left | \začiatok(zarovnané) & u=6x+1; \; du=6dx.\\ & dv=e^(7x)dx; \; v=\frac(e^(7x))(7). \end(zarovnané) \right |=\\ =\frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \left ((6x+1) \cdot\frac(e^(7x))(7) - \int\frac(e^(7x))(7)\cdot 6\;dx \right)=\\ =\frac((3x^2+ x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6)(49)\cdot\int\ e^(7x)\; dx=\\ =\frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6)(49 )\cdot\frac(e^(7x))(7)+C=\\ =\frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e ^(7x))(49) +\frac(6\; e^(7x))(343)+C. $$

Výslednú odpoveď je možné zjednodušiť otvorením zátvoriek a preskupením výrazov:

$$ \frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6\; e^(7x ))(343)+C=e^(7x)\cdot \left(\frac(3x^2)(7)+\frac(x)(49)-\frac(1)(343) \right)+ C. $$

Odpoveď: $\int (3x^2+x) e^(7x) \; dx=e^(7x)\cdot \left(\frac(3x^2)(7)+\frac(x)(49)-\frac(1)(343) \right)+C$.

Príklad č.5

Nájsť $\int (x^2+5)\sin(3x+1) \; dx$.

Tu, rovnako ako v predchádzajúcom príklade, sa integrácia podľa častí aplikuje dvakrát. Podrobné vysvetlenia boli uvedené skôr, takže uvediem iba riešenie:

$$ \int (x^2+5)\sin(3x+1) \; dx=\left | \begin(zarovnané) & u=x^2+5; \; du=2xdx.\\ & dv=\sin(3x+1)dx; \; v=-\frac(\cos(3x+1))(3). \end(zarovnané) \right |=\\ =(x^2+5)\cdot \left(-\frac(\cos(3x+1))(3) \right)-\int\left(-\ frac(\cos(3x+1))(3) \vpravo)\cdot 2xdx=\\ = -\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac (2)(3)\int x\cos(3x+1)dx= \vľavo | \begin(zarovnané) & u=x; \; du=dx.\\ & dv=\cos(3x+1)dx; \; v=\frac(\sin(3x+1))(3). \end(zarovnané) \right |=\\ =-\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac(2)(3)\cdot \left( x\cdot\frac(\sin(3x+1))(3)-\int\frac(\sin(3x+1))(3)dx \right)=\\ =-\frac((x^2) +5)\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac(2)(9)\cdot\int\sin(3x+ 1 )dx=\\ =-\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac ( 2)(9)\cdot \left(-\frac(\cos(3x+1))(3)\right)+C=\\ = -\frac((x^2+5)\cdot\cos ( 3x+1))(3) +\frac(2x\sin(3x+1))(9)+\frac(2\cos(3x+1))(27)+C=\\ =-\frac ( x^2\cdot\cos(3x+1))(3)-\frac(5\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9) +\frac(2\cos(3x+1))(27)+C=\\ =-\frac(x^2\cdot\cos(3x+1))(3) +\frac(2x\sin ( 3x+1))(9)-\frac(43\cos(3x+1))(27)+C. $$

Odpoveď: $\int (x^2+5)\sin(3x+1) \; dx=-\frac(x^2\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac(43\cos(3x+1) )(27) + C$.

Aplikácia metódy integrácie po častiach v trochu neštandardných prípadoch, na ktoré sa nevzťahujú pravidlá č.1 a č.2 bude uvedená v r.

Kalkulačka rieši integrály s popisom akcií DETAIL v ruštine a zadarmo!

Riešenie neurčitých integrálov

Toto je online služba v jeden krok:

Riešenie určitých integrálov

Toto je online služba v jeden krok:

• Zadajte výraz integrand (integrálna funkcia)
• Zadajte dolnú hranicu integrálu
• Zadajte hornú hranicu integrálu

Riešenie dvojitých integrálov

• Zadajte výraz integrand (integrálna funkcia)

Riešenie nesprávnych integrálov

• Zadajte výraz integrand (integrálna funkcia)
• Zadajte hornú oblasť integrácie (alebo + nekonečno)
• Zadajte dolnú oblasť integrácie (alebo - nekonečno)

Ísť do: Online služba "Nevlastný integrál" →

Riešenie trojných integrálov

• Zadajte výraz integrand (integrálna funkcia)
• Zadajte dolné a horné limity pre prvý integračný región
• Zadajte dolný a horný limit pre druhú integračnú oblasť
• Zadajte dolnú a hornú hranicu pre tretí región integrácie

Ísť do: Online služba "Trojitý integrál" →

Táto služba vám umožňuje skontrolovať vaše výpočty za správnosť

možnosti

• Podporuje všetky možné matematické funkcie: sínus, kosínus, exponent, tangens, kotangens, druhé a kubické odmocniny, mocniny, exponenciály a iné.
• Existujú príklady vstupu, a to ako pre neurčité integrály, tak aj pre nevlastné a určité.
• Opravuje chyby vo výrazoch, ktoré zadávate, a ponúka vlastné možnosti vstupu.
• Numerické riešenie pre určité a nevlastné integrály (vrátane dvojných a trojných integrálov).
• Podpora komplexných čísel, ako aj rôznych parametrov (vo výraze integrand môžete zadať nielen integračnú premennú, ale aj ďalšie premenné parametrov)

Integrácia po častiach. Príklady riešení

Ahoj zas. Dnes sa v lekcii naučíme, ako integrovať po častiach. Metóda integrácie po častiach je jedným zo základných kameňov integrálneho počtu. Počas testov alebo skúšok sú študenti takmer vždy požiadaní, aby vyriešili nasledujúce typy integrálov: najjednoduchší integrál (pozri článok) alebo integrál nahradením premennej (pozri článok) alebo je integrál práve zapnutý integrácia metódou častí.

Ako vždy, mali by ste mať po ruke: Tabuľka integrálov A Tabuľka derivátov. Ak ich ešte nemáte, navštívte prosím úschovňu mojej webovej stránky: Matematické vzorce a tabuľky. Nebudem sa unavovať opakovaním – je lepšie si všetko vytlačiť. Pokúsim sa prezentovať všetok materiál dôsledne, jednoducho a jasne, pri integrácii častí nie sú žiadne zvláštne ťažkosti.

Aký problém rieši metóda integrácie po častiach? Metóda integrácie po častiach rieši veľmi dôležitý problém, umožňuje integrovať niektoré funkcie, ktoré nie sú v tabuľke, práca funkcie av niektorých prípadoch dokonca aj kvocienty. Ako si pamätáme, neexistuje žiadny vhodný vzorec: . Ale je tu tento: – vzorec pre integráciu po častiach osobne. Viem, viem, si jediný – budeme s ňou pracovať počas celej hodiny (teraz je to jednoduchšie).

A hneď zoznam do štúdia. Integrály nasledujúcich typov sú prevzaté časťami:

1) , , – logaritmus, logaritmus vynásobený nejakým polynómom.

2) ,je exponenciálna funkcia vynásobená nejakým polynómom. Patria sem aj integrály ako - exponenciálna funkcia vynásobená polynómom, ale v praxi je to 97 percent, pod integrálom je pekné písmeno „e“. ... článok je trochu lyrický, ach áno ... prišla jar.

3) , , sú goniometrické funkcie vynásobené nejakým polynómom.

4) , – inverzné goniometrické funkcie („oblúky“), „oblúky“ vynásobené nejakým polynómom.

Niektoré zlomky sa berú aj po častiach, podrobne zvážime aj zodpovedajúce príklady.

Integrály logaritmov

Príklad 1

klasické. Z času na čas sa tento integrál nájde v tabuľkách, ale nie je vhodné použiť hotovú odpoveď, pretože učiteľ má jarný nedostatok vitamínov a bude ťažko nadávať. Pretože uvažovaný integrál nie je v žiadnom prípade tabuľkový - berie sa po častiach. Rozhodujeme sa:

Pre medziľahlé vysvetlenia prerušujeme riešenie.

Používame vzorec integrácie podľa častí:

Vzorec sa aplikuje zľava doprava

Pozeráme sa na ľavú stranu: . Je zrejmé, že v našom príklade (a vo všetkých ostatných, ktoré budeme zvažovať) musí byť niečo označené ako , a niečo ako .

V integráloch uvažovaného typu sa vždy označuje logaritmus.

Technicky je návrh riešenia realizovaný nasledovne, do stĺpca zapíšeme:

To znamená, že sme označili logaritmus a - zvyšná časť integrandový výraz.

Ďalšia fáza: nájdite rozdiel:

Diferenciál je takmer to isté ako derivácia; o tom, ako ho nájsť, sme už diskutovali v predchádzajúcich lekciách.

Teraz nájdeme funkciu. Aby ste našli funkciu, ktorú potrebujete integrovať pravá strana nižšia rovnosť:

Teraz otvoríme naše riešenie a zostrojíme pravú stranu vzorca: .
Mimochodom, tu je ukážka konečného riešenia s niekoľkými poznámkami:

Jediným bodom v práci je, že som okamžite prehodil a , keďže je zvykom písať faktor pred logaritmus.

Ako vidíte, použitie vzorca integrácie podľa častí v podstate zredukovalo naše riešenie na dva jednoduché integrály.

Upozorňujeme, že v niektorých prípadoch hneď po pri použití vzorca sa zjednodušenie nevyhnutne vykoná pod zvyšným integrálom - v uvažovanom príklade sme integrand zredukovali na „x“.

Skontrolujme to. Aby ste to dosiahli, musíte použiť derivát odpovede:

Pôvodná funkcia integrandu bola získaná, čo znamená, že integrál bol vyriešený správne.

Počas testu sme použili pravidlo diferenciácie produktov: . A to nie je náhoda.

Vzorec na integráciu podľa častí a vzorec – sú to dve vzájomne inverzné pravidlá.

Príklad 2

Nájdite neurčitý integrál.

Integrand je súčinom logaritmu a polynómu.
Rozhodnime sa.

Ešte raz podrobne opíšem postup uplatňovania pravidla, v budúcnosti budú príklady uvedené stručnejšie a ak máte problémy s riešením sami, musíte sa vrátiť k prvým dvom príkladom lekcie .

Ako už bolo spomenuté, je potrebné označiť logaritmus (na tom, že ide o mocninu nezáleží). Označujeme podľa zvyšná časť integrandový výraz.

Do stĺpca píšeme:

Najprv nájdeme diferenciál:

Tu používame pravidlo na diferenciáciu komplexnej funkcie . Nie je náhoda, že hneď na prvej lekcii témy Neurčitý integrál. Príklady riešení Zameral som sa na to, že na zvládnutie integrálov je potrebné „dostať do rúk“ derivácie. S derivátmi sa budete musieť vysporiadať viackrát.

Teraz nájdeme funkciu, na ktorú sa integrujeme pravá strana nižšia rovnosť:

Na integráciu sme použili najjednoduchší tabuľkový vzorec

Teraz je všetko pripravené na aplikáciu vzorca . Otvorte hviezdičkou a „zostavte“ riešenie v súlade s pravou stranou:

Pod integrálom máme opäť polynóm pre logaritmus! Preto sa riešenie opäť preruší a druhýkrát sa použije pravidlo integrácie po častiach. Nezabudnite, že v podobných situáciách sa vždy označuje logaritmus.

Bolo by dobré, keby ste už vedeli nájsť najjednoduchšie integrály a derivácie ústne.

(1) Nenechajte sa zmiasť znameniami! Veľmi často sa tu stráca mínus, tiež si všimnite, že mínus sa týka všetkým držiak a tieto zátvorky je potrebné správne rozbaliť.

(2) Otvorte držiaky. Posledný integrál zjednodušíme.

(3) Vezmeme posledný integrál.

(4) „Prečesanie“ odpovede.

Potreba aplikovať pravidlo integrácie po častiach dvakrát (alebo dokonca trikrát) nevzniká veľmi zriedkavo.

A teraz pár príkladov pre vaše vlastné riešenie:

Príklad 3

Nájdite neurčitý integrál.

Tento príklad je vyriešený zmenou premennej (alebo jej dosadením pod diferenciálne znamienko)! Prečo nie - môžete to skúsiť po častiach, ukáže sa to ako vtipná vec.

Príklad 4

Nájdite neurčitý integrál.

Ale tento integrál je integrovaný po častiach (sľúbený zlomok).

Toto sú príklady, ktoré môžete vyriešiť sami, riešenia a odpovede na konci hodiny.

Zdá sa, že v príkladoch 3 a 4 sú integrandy podobné, ale metódy riešenia sú odlišné! Toto je hlavná náročnosť zvládnutia integrálov – ak zvolíte nesprávnu metódu riešenia integrálu, môžete sa v ňom hrabať celé hodiny ako v skutočnej hádanke. Preto čím viac budete riešiť rôzne integrály, tým lepšie, tým ľahšie bude test a skúška. Navyše v druhom ročníku budú diferenciálne rovnice a bez skúseností s riešením integrálov a derivácií tam nie je čo robiť.

Z hľadiska logaritmu je to pravdepodobne viac než dosť. Okrem toho si pamätám, že študenti inžinierstva používajú logaritmy na označenie ženských pŕs =). Mimochodom, je užitočné poznať naspamäť grafy hlavných elementárnych funkcií: sínus, kosínus, arkustangens, exponent, polynómy tretieho, štvrtého stupňa atď. Nie, samozrejme, kondóm na svete
Nebudem to naťahovať, ale teraz si budete veľa pamätať z tejto sekcie Grafy a funkcie =).

Integrály exponenciály násobené polynómom

Všeobecné pravidlo:

Príklad 5

Nájdite neurčitý integrál.

Pomocou známeho algoritmu integrujeme po častiach:

Ak máte problémy s integrálom, mali by ste sa vrátiť k článku Metóda zmeny premennej v neurčitom integráli.

Jediná ďalšia vec, ktorú môžete urobiť, je upraviť odpoveď:

Ak však vaša technika výpočtu nie je príliš dobrá, potom najziskovejšou možnosťou je nechať ju ako odpoveď alebo dokonca

To znamená, že príklad sa považuje za vyriešený, keď sa vezme posledný integrál. Nebude to chyba, iná vec je, že vás učiteľ môže požiadať o zjednodušenie odpovede.

Príklad 6

Nájdite neurčitý integrál.

Toto je príklad, ktorý môžete vyriešiť sami. Tento integrál je integrovaný dvakrát po častiach. Osobitná pozornosť by sa mala venovať znakom - je ľahké sa v nich zmiasť, pamätáme si tiež, že ide o komplexnú funkciu.

Viac k vystavovateľovi niet čo povedať. Len dodám, že exponenciála a prirodzený logaritmus sú vzájomne inverzné funkcie, toto som ja na tému zábavných grafov vyššej matematiky =) Zastav sa, prestaň, neboj sa, prednášajúci je triezvy.

Integrály goniometrických funkcií násobené polynómom

Všeobecné pravidlo: lebo vždy označuje polynóm

Príklad 7

Nájdite neurčitý integrál.

Poďme integrovať po častiach:

Hmmm...a nie je čo komentovať.

Príklad 8

Nájdite neurčitý integrál

Toto je príklad, aby ste si sami vyriešili

Príklad 9

Nájdite neurčitý integrál

Ďalší príklad so zlomkom. Rovnako ako v dvoch predchádzajúcich príkladoch, for označuje polynóm.

Poďme integrovať po častiach:

Ak máte nejaké ťažkosti alebo nedorozumenia s hľadaním integrálu, odporúčam lekciu navštíviť Integrály goniometrických funkcií.

Príklad 10

Nájdite neurčitý integrál

Toto je príklad, ktorý môžete vyriešiť sami.

Tip: Pred použitím metódy integrácie podľa častí by ste mali použiť nejaký trigonometrický vzorec, ktorý premení súčin dvoch goniometrických funkcií na jednu funkciu. Vzorec možno použiť aj pri aplikácii metódy integrácie po častiach, podľa toho, čo je pre vás výhodnejšie.

To je v tomto odseku asi všetko. Z nejakého dôvodu som si spomenul na vetu z fyzikálnej a matematickej hymny „A sínusový graf prebieha vlnu po vlne pozdĺž osi x“.

Integrály inverzných goniometrických funkcií.
Integrály inverzných goniometrických funkcií násobené polynómom

Všeobecné pravidlo: vždy označuje inverznú goniometrickú funkciu.

Dovoľte mi pripomenúť, že inverzné goniometrické funkcie zahŕňajú arkussínus, arkussínus, arkustangens a arkkotangens. Pre stručnosť záznamu ich budem nazývať „oblúky“

Metóda integrácie po častiach sa používa najmä vtedy, keď integrand pozostáva zo súčinu dvoch faktorov určitého typu. Vzorec integrácie podľa častí vyzerá takto:

Umožňuje zredukovať výpočet daného integrálu
na výpočet integrálu
, ktorý sa ukazuje byť jednoduchší ako tento.

Väčšinu integrálov vypočítaných metódou integrácie po častiach možno rozdeliť do troch skupín:

1. Integrály formulára
,
,
, Kde
- polynóm,
– číslo, ktoré sa nerovná nule

V tomto prípade cez označujú polynóm

.

2. Integrály formulára
,
,
,
,
, Kde
– polynóm.

V tomto prípade cez
označovať
, a zvyšok integrandu cez :

3. Integrály formulára
,
, Kde
– čísla.

V tomto prípade cez označovať
a použiť vzorec integrácie podľa častí dvakrát, čím sa vrátime k pôvodnému integrálu, po ktorom sa pôvodný integrál vyjadrí z rovnosti.

Komentujte: V niektorých prípadoch je potrebné na nájdenie daného integrálu použiť vzorec integrácie podľa častí niekoľkokrát. Tiež metóda integrácie po častiach je kombinovaná s inými metódami.

Príklad 26.

Nájdite integrály pomocou metódy po častiach: a)
; b)
.

Riešenie.

b)

3.1.4. Integrácia zlomkovo-racionálnych funkcií

Zlomková racionálna funkcia(racionálny zlomok) je funkcia rovnajúca sa podielu dvoch polynómov:
, Kde
– polynóm stupňa
,
– polynóm stupňa .

Racionálny zlomok sa nazýva správne, ak je stupeň mnohočlenu v čitateli menší ako stupeň mnohočlenu v menovateli, t.j.
, inak (ak
) racionálny zlomok sa nazýva nesprávne.

Akýkoľvek nesprávny racionálny zlomok môže byť reprezentovaný ako súčet polynómu
a vlastný racionálny zlomok delením čitateľa menovateľom podľa pravidla na delenie polynómov:

,

Kde
– celá časť z divízie, - správny racionálny zlomok,
- zvyšok divízie.

Správne racionálne zlomky formulára:

ja ;

II.
;

III.
;

IV.
,

Kde ,,
,
,,,
– reálne čísla a
(t.j. štvorcová trojčlenka v menovateli zlomkov III a IV nemá korene - diskriminant je záporný) sú tzv. jednoduché racionálne zlomky I, II, III a IV typy.

Integrácia jednoduchých zlomkov

Integrály najjednoduchších zlomkov štyroch typov sa vypočítajú nasledovne.

ja)
.

II),
.

III) Ak chcete integrovať najjednoduchší zlomok typu III, vyberte celý štvorec v menovateli a nahraďte ho
. Po substitúcii sa integrál rozdelí na dva integrály. Prvý integrál sa vypočíta izoláciou derivácie menovateľa v čitateli, čím sa získa tabuľkový integrál, a druhý integrál sa prevedie do tvaru
, pretože
, čo dáva aj tabuľkový integrál.

;

IV) Ak chcete integrovať najjednoduchší zlomok typu IV, vyberte úplný štvorec v menovateli a nahraďte ho
. Po substitúcii sa integrál rozdelí na dva integrály. Prvý integrál sa vypočíta substitúciou
a druhý pomocou rekurentných vzťahov.

Príklad 27.

Nájdite integrály jednoduchých zlomkov:

A)
; b)
; V)
.

Riešenie.

A)
.

Akýkoľvek správny racionálny zlomok, ktorého menovateľ možno rozdeliť na faktor, možno znázorniť ako súčet jednoduchých zlomkov. Rozklad na súčet jednoduchých zlomkov sa uskutočňuje metódou neurčitých koeficientov. Je to nasledovné:

zodpovedá jednému zlomku formulára ;

– každý faktor menovateľa
zodpovedá sume zlomky formulára

zodpovedá zlomku formy
;

– každý štvorcový faktor menovateľa
zodpovedá sume zlomky formulára

kde sú neurčené koeficienty.

Na nájdenie neurčitých koeficientov sa pravá strana vo forme súčtu jednoduchých zlomkov privedie k spoločnému menovateľovi a transformuje sa. Výsledkom je zlomok s rovnakým menovateľom ako na ľavej strane rovnice. Potom sa menovatelia zahodia a čitatelia sa vyrovnajú. Výsledkom je identická rovnosť, v ktorej ľavá strana je polynóm so známymi koeficientmi a pravá strana je polynóm s neznámymi koeficientmi.

Existujú dva spôsoby, ako určiť neznáme koeficienty: metóda neznámych koeficientov a metóda parciálnych hodnôt.

Metóda neurčených koeficientov.

Pretože polynómy sú identicky rovnaké, potom sú koeficienty pri rovnakých mocninách rovnaké . Rovnaké koeficienty v rovnakých stupňoch v polynómoch ľavej a pravej strany získame sústavu lineárnych rovníc. Pri riešení sústavy určujeme neisté koeficienty.

Metóda súkromných hodnôt.

Pretože polynómy sú identicky rovnaké, teda dosadzovanie na ľavú a pravú stranu ľubovoľného čísla získame skutočnú rovnosť, lineárnu vzhľadom na neznáme koeficienty. Nahradením toľkých hodnôt , koľko neznámych koeficientov je, získame sústavu lineárnych rovníc. Namiesto Na ľavú a pravú stranu môžete dosadiť ľubovoľné čísla, ale pohodlnejšie je nahradiť korene menovateľov zlomkov.

Po nájdení hodnôt neznámych koeficientov sa pôvodný zlomok zapíše ako súčet jednoduchých zlomkov v integrande a nad každým jednoduchým zlomkom sa vykoná predtým diskutovaná integrácia.

Integračná schéma racionálne zlomky:

1. Ak je integrand nevlastný, potom je potrebné ho prezentovať ako súčet polynómu a vlastného racionálneho zlomku (t. j. vydeliť polynóm čitateľa polynómom menovateľa so zvyškom). Ak je integrand správny, okamžite prejdeme k druhému bodu diagramu.

2. Ak je to možné, vynásobte menovateľa vlastného racionálneho zlomku.

3. Rozlož vlastný racionálny zlomok na súčet jednoduchých racionálnych zlomkov metódou neurčitých koeficientov.

4. Integrujte výsledný súčet polynómu a jednoduchých zlomkov.

Príklad 28.

Nájdite integrály racionálnych zlomkov:

A)
; b)
; V)
.

Riešenie.

A)
.

Pretože integrand je nevlastný racionálny zlomok, potom vyberieme celú časť, t.j. Predstavme si to ako súčet polynómu a vlastného racionálneho zlomku. Vydeľte polynóm v čitateli polynómom v menovateli pomocou rohu.

Pôvodný integrál bude mať tvar:
.

Rozložme vlastný racionálny zlomok na súčet jednoduchých zlomkov metódou neurčitých koeficientov:

, dostaneme:

Riešením systému lineárnych rovníc získame hodnoty neistých koeficientov: A = 1; IN = 3.

Potom má požadované rozšírenie tvar:
.

=
.

b)
.

.

Zahoďme menovateľov a prirovnajme ľavú a pravú stranu:

Rovnaké koeficienty v rovnakých stupňoch , dostaneme systém:

Riešením systému piatich lineárnych rovníc nájdeme neurčené koeficienty:

.

Nájdite pôvodný integrál, berúc do úvahy výsledné rozšírenie:

.

V)
.

Rozviňme integrand (vlastný racionálny zlomok) na súčet jednoduchých zlomkov pomocou metódy neurčitých koeficientov. Hľadáme rozklad v tvare:

.

Redukovaním na spoločného menovateľa dostaneme:

Zahoďme menovateľov a prirovnajme ľavú a pravú stranu:

Na nájdenie neistých koeficientov použijeme metódu parciálnych hodnôt. Pridajme čiastkové hodnoty, pri ktorých faktory miznú, t.j. tieto hodnoty dosadíme do posledného výrazu a dostaneme tri rovnice:

;
;

;
;

;
.

Potom má požadované rozšírenie tvar:

Nájdite pôvodný integrál, berúc do úvahy výsledné rozšírenie:

Nasledujúci vzorec je tzv vzorec integrácie podľa častí v neurčitom integráli:

Ak chcete použiť vzorec integrácie podľa častí, integrand sa musí rozdeliť na dva faktory. Jeden z nich je označený u a zvyšok sa vzťahuje na druhý faktor a je označený dv. Potom diferenciáciou nájdeme du a integrácia – funkcia v. Zároveň za u dv- taká časť integrandu, ktorú možno ľahko integrovať.

Kedy je výhodné použiť metódu integrácie po častiach? Potom, keď integrand obsahuje :

1) - logaritmické funkcie, ako aj inverzné goniometrické funkcie (s predponou „oblúk“), potom na základe dlhodobých skúseností s integráciou po častiach sa tieto funkcie označujú u;

2) , , - sínus, kosínus a exponent násobené P(X) je ľubovoľný polynóm v x, potom tieto funkcie označíme dv, a polynóm je cez u;

3) , , , , v tomto prípade sa integrácia po častiach aplikuje dvakrát.

Vysvetlime hodnotu metódy integrácie po častiach na príklade prvého prípadu. Nech výraz pod znamienkom integrálu obsahuje logaritmickú funkciu (toto bude príklad 1). Použitím integrácie po častiach sa takýto integrál redukuje na výpočet integrálu iba algebraických funkcií (najčastejšie polynómu), to znamená, že neobsahuje logaritmickú alebo inverznú goniometrickú funkciu. Použitie vzorca integrácie podľa častí uvedeného na samom začiatku hodiny

získame v prvom člene (bez integrálu) logaritmickú funkciu a v druhom člene (pod znakom integrálu) funkciu, ktorá logaritmus neobsahuje. Integrál algebraickej funkcie je oveľa jednoduchší ako integrál, pod ktorého znamienkom sa nachádza logaritmická alebo inverzná goniometrická funkcia samostatne alebo spolu s algebraickým faktorom.

Teda pomocou integrácia podľa vzorcov častí integrácia sa nevykoná okamžite: nájdenie daného integrálu sa redukuje na nájdenie iného. Význam vzorca integrácie podľa častí je, že v dôsledku jeho aplikácie sa nový integrál ukáže ako tabuľkový alebo sa aspoň stane jednoduchším ako pôvodný.

Metóda integrácie po častiach je založená na použití vzorca na rozlíšenie súčinu dvoch funkcií:

potom to môže byť napísané vo forme

ktorý bol daný na samom začiatku hodiny.

Pri hľadaní integrovaním funkcie v tým sa získa nekonečná množina primitívnych funkcií. Ak chcete použiť vzorec integrácie podľa častí, môžete použiť ktorýkoľvek z nich, a teda ten, ktorý zodpovedá ľubovoľnej konštante S, rovná nule. Preto pri hľadaní funkcie vľubovoľná konštanta S by sa nemalo zadávať.

Metóda integrácie po častiach má veľmi špeciálne uplatnenie: možno ju použiť na odvodenie opakujúcich sa vzorcov na hľadanie primitívnych funkcií, keď je potrebné znížiť stupeň funkcií pod znamienkom integrálu. Zníženie stupňa je nevyhnutné, keď neexistujú žiadne tabuľkové integrály napríklad pre funkcie, ako sú sínusy a kosínusy, na mocniny väčšie ako druhá a ich súčin. Opakujúci sa vzorec je vzorec na nájdenie ďalšieho člena postupnosti cez predchádzajúci člen. V indikovaných prípadoch sa cieľ dosiahne postupným znižovaním stupňa. Takže, ak je integrand sínus ku štvrtej mocnine x, potom integráciou po častiach môžete nájsť vzorec pre integrál sínus ku tretej mocnine atď. Posledný odsek tejto lekcie je venovaný opísanej úlohe.

Použitie integrácie po častiach spolu

Príklad 1. Nájdite neurčitý integrál pomocou metódy integrácie po častiach:

Riešenie. Vo výraze integrand - logaritmus, ktorý, ako už vieme, možno rozumne označiť u. Veríme, že,.

Nájdeme (ako už bolo uvedené vo vysvetlení k teoretickému odkazu, okamžite získame logaritmickú funkciu v prvom člene (bez integrálu) a funkciu, ktorá neobsahuje logaritmus v druhom člene (pod znakom integrálu):

A opäť logaritmus...

Príklad 2 Nájdite neurčitý integrál:

Riešenie. Nechajte,.

Logaritmus je prítomný v štvorci. To znamená, že je potrebné ju diferencovať ako komplexnú funkciu. nachádzame
,
.

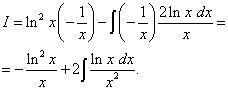
Opäť nájdeme druhý integrál po častiach a získame už spomínanú výhodu (v prvom člene (bez integrálu) je logaritmická funkcia a v druhom člene (pod znamienkom integrálu) je funkcia, ktorá neobsahuje logaritmus).

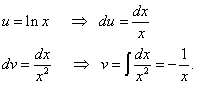
Nájdeme pôvodný integrál:

Príklad 3

Riešenie. Arkustangens, podobne ako logaritmus, je lepšie označovať u. Tak nech,.

potom ,
.

Použitím vzorca integrácie podľa častí dostaneme:

Druhý integrál nájdeme zmenou premennej.

Návrat k premennej X, dostaneme

.

Nájdeme pôvodný integrál:

.

Príklad 4. Nájdite neurčitý integrál pomocou metódy integrácie po častiach:

Riešenie. Je lepšie označovať exponent podľa dv. Integrand sme rozdelili na dva faktory. Veriť tomu

Príklad 5. Nájdite neurčitý integrál pomocou metódy integrácie po častiach:

.

Riešenie. Nechajte,. Potom, .

Pomocou vzorca integrácie podľa častí (1) nájdeme:

Príklad 6. Nájdite neurčitý integrál integráciou po častiach:

Riešenie. Sínus, podobne ako exponenciálu, možno vhodne označiť dv. Nechajte,.

Pomocou vzorca integrácie podľa častí nájdeme:

Opäť aplikujeme integráciu po častiach spolu

Príklad 10. Nájdite neurčitý integrál integráciou po častiach:

.

Riešenie. Ako vo všetkých podobných prípadoch je vhodné označovať kosínus podľa dv. Označujeme,.

Potom , .

Pomocou vzorca integrácie podľa častí získame:

Integráciu po častiach aplikujeme aj na druhý termín. Označujeme,.

Pomocou týchto zápisov integrujeme uvedený výraz:

Teraz nájdeme požadovaný integrál:

Medzi integrály, ktoré je možné riešiť metódou integrácie po častiach, patria aj také, ktoré nie sú zaradené do žiadnej z troch skupín uvedených v teoretickej časti, pre ktoré je z praxe známe, že je lepšie označovať u, a čo cez dv. Preto v týchto prípadoch musíte vziať do úvahy pohodlie, ktoré je tiež uvedené v odseku „Podstata metódy integrácie po častiach“: napr. u treba zobrať časť integrandu, ktorá sa pri diferenciácii veľmi neskomplikuje, ale dv- taká časť integrandu, ktorú možno ľahko integrovať. Posledným príkladom tejto lekcie je riešenie práve takéhoto integrálu.