අනුකෘතියේ eigenvalues ​​සහ eigenvectors සොයන්න. න්‍යාස සහ දෛශික

"පළමු කොටසෙහි රසායන විද්‍යාව අවබෝධ කර ගැනීම සඳහා අවම වශයෙන් අවශ්‍ය ප්‍රතිපාදන දක්වා ඇති අතර, දෙවන කොටසෙහි බහුවිචල්‍ය විශ්ලේෂණ ක්‍රම පිළිබඳ ගැඹුරු අවබෝධයක් සඳහා ඔබ දැනගත යුතු කරුණු අඩංගු වේ. ඉදිරිපත් කිරීම Excel වැඩපොතෙහි ඇති උදාහරණ සමඟ නිදර්ශනය කර ඇත. Matrix.xls, මෙම ලේඛනය සමඟ ඇති.

උදාහරණ සඳහා සබැඳි එක්සෙල් වස්තූන් ලෙස පෙළෙහි තබා ඇත. මෙම උදාහරණ ස්වභාවයෙන්ම වියුක්ත ය; රසායන විද්‍යාවේදී න්‍යාස වීජ ගණිතය භාවිතය පිළිබඳ සැබෑ ජීවිතයේ උදාහරණ විවිධ රසායන විද්‍යාත්මක යෙදුම් ආවරණය වන වෙනත් පාඨවල සාකච්ඡා කෙරේ.

විශ්ලේෂණ රසායන විද්‍යාවේ සිදු කරන බොහෝ මිනුම් සෘජු නොවේ, නමුත් වක්ර. මෙයින් අදහස් කරන්නේ අත්හදා බැලීමේදී අපේක්ෂිත විශ්ලේෂණ C (සාන්ද්‍රණය) අගය වෙනුවට වෙනත් අගයක් ලැබෙන බවයි. x(සංඥා), සම්බන්ධ නමුත් C ට සමාන නොවේ, i.e. x(C) ≠ C. රීතියක් ලෙස, යැපීම් වර්ගය x(C) නොදන්නා නමුත් වාසනාවකට මෙන් විශ්ලේෂණ රසායන විද්‍යාවේ බොහෝ මිනුම් සමානුපාතික වේ. මෙයින් අදහස් කරන්නේ C හි සාන්ද්‍රණය වැඩි වීමත් සමඟ ය aවාර, සංඥා X එකම ප්‍රමාණයකින් වැඩි වනු ඇත, i.e. x(a C) = x(C) ඊට අමතරව, සංඥා ද ආකලන වේ, එබැවින් C 1 සහ C 2 සාන්ද්‍රණය සහිත ද්‍රව්‍ය දෙකක් ඇති නියැදියක සංඥාව එක් එක් සංරචකයේ සංඥා එකතුවට සමාන වේ, i.e. x(C 1 + C 2) = x(C 1)+ x(C 2). සමානුපාතිකත්වය සහ ආකලන එක්ව ලබා දෙයි රේඛීයත්වය. රේඛීයත්වයේ මූලධර්මය නිදර්ශනය කිරීම සඳහා බොහෝ උදාහරණ ලබා දිය හැකි නමුත් වඩාත් කැපී පෙනෙන උදාහරණ දෙක - වර්ණදේහ සහ වර්ණාවලීක්ෂය සඳහන් කිරීම ප්රමාණවත්ය. විශ්ලේෂණ රසායන විද්‍යාවේ අත්හදා බැලීමක ආවේනික වූ දෙවන ලක්ෂණය වේ බහු නාලිකා. නවීන විශ්ලේෂණ උපකරණ එකවර බොහෝ නාලිකා සඳහා සංඥා මනිනු ලබයි. නිදසුනක් ලෙස, ආලෝක සම්ප්රේෂණයේ තීව්රතාවය එකවර තරංග ආයාම කිහිපයක් සඳහා මනිනු ලැබේ, i.e. වර්ණාවලිය. එමනිසා, අත්හදා බැලීමේදී අපි බොහෝ සංඥා සමඟ කටයුතු කරමු x 1 , x 2 ,...., x n, අධ්‍යයනය යටතේ පවතින පද්ධතියේ පවතින ද්‍රව්‍යවල C 1, C 2, ..., C m සාන්ද්‍රණ කට්ටලය ගුනාංගීකරනය කිරීම.

සහල්. 1 වර්ණාවලි

එබැවින්, විශ්ලේෂණාත්මක පරීක්ෂණයක් රේඛීයත්වය සහ බහුමානත්වය මගින් සංලක්ෂිත වේ. එබැවින්, පර්යේෂණාත්මක දත්ත දෛශික සහ න්‍යාස ලෙස සලකා ඒවා න්‍යාස වීජ ගණිතයේ උපකරණය භාවිතයෙන් හැසිරවීම පහසු වේ. 4000 සිට 4796 cm −1 දක්වා තරංග ආයාම 200 කින් ගත් වර්ණාවලි තුනක් ඉදිරිපත් කරන උදාහරණයෙන් මෙම ප්‍රවේශයේ ඵලදායිත්වය විදහා දක්වයි. A සහ B ද්‍රව්‍ය දෙකක සාන්ද්‍රණය දන්නා සම්මත සාම්පල සඳහා පළමු (x 1) සහ දෙවන (x 2) වර්ණාවලි ලබා ගන්නා ලදී: පළමු නියැදියේ [A] = 0.5, [B] = 0.1, සහ දෙවන නියැදිය [A] = 0.2, [B] = 0.6. x 3 ලෙස නම් කර ඇති වර්ණාවලියේ නව, නොදන්නා නියැදියක් ගැන කුමක් කිව හැකිද?

අපි 200 මානයේ දෛශික තුනක් ලෙස පර්යේෂණාත්මක වර්ණාවලි තුනක් සලකා බලමු. රේඛීය වීජ ගණිතය භාවිතයෙන්, අපට පහසුවෙන් පෙන්විය හැක්කේ x 3 = 0.1 x 1 +0.3 x 2, එබැවින් තුන්වන නියැදියේ A ද්‍රව්‍ය පමණි. සහ B පැහැදිලිවම [A] = 0.5×0.1 + 0.2×0.3 = 0.11 සහ [B] = 0.1×0.1 + 0.6×0.3 = 0.19 සාන්ද්‍රණයන්හි පවතී.

1. මූලික තොරතුරු 1.1 න්‍යාස

Matrixඋදාහරණයක් ලෙස, සෘජුකෝණාස්රාකාර සංඛ්යා වගුවක් ලෙස හැඳින්වේ

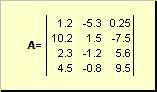
සහල්. 2 Matrix

න්‍යාස විශාල තද අකුරු (A) මගින් ද, ඒවායේ මූලද්‍රව්‍ය දර්ශක සමඟ අනුරූප කුඩා අකුරු මගින් ද දැක්වේ, i.e. a ij පළමු දර්ශකය පේළි අංක, සහ දෙවන - තීරු. රසායන විද්‍යාවේදී, සුචියක උපරිම අගය දර්ශකයට සමාන අකුරකින්, නමුත් ලොකු අකුරින් දැක්වීම සිරිතකි. එබැවින් A matrix ලෙසද ලිවිය හැක ( a ij , i = 1,..., අයි; j = 1,..., ජේ) උදාහරණයක් matrix සඳහා අයි = 4, ජේ= 3 සහ a 23 = −7.5.

අංක යුගලය අයිසහ ජේන්‍යාසයේ මානය ලෙස හඳුන්වනු ලබන අතර එය ලෙස දැක්වේ අයි× ජේ. රසායන විද්‍යාවේ න්‍යාසයකට උදාහරණයක් ලෙස ලබාගත් වර්ණාවලි කට්ටලයකි අයිසඳහා සාම්පල ජේතරංග ආයාමයන්.

1.2 matrices සමඟ සරලම මෙහෙයුම්

Matrices විය හැක සංඛ්යා මගින් ගුණ කරන්න. මෙම අවස්ථාවේදී, එක් එක් මූලද්රව්යය මෙම සංඛ්යාවෙන් ගුණ කරනු ලැබේ. උදාහරණ වශයෙන් -

සහල්. 3 න්‍යාසයක් සංඛ්‍යාවකින් ගුණ කිරීම

එකම මානයක න්‍යාස දෙකක් මූලද්‍රව්‍යයෙන් මූලද්‍රව්‍ය විය හැක ගුණ කරන්නසහ අඩු කරන්න. උදාහරණ වශයෙන්,

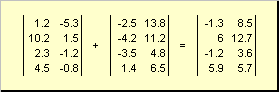
සහල්. 4 Matrix එකතු කිරීම

සංඛ්‍යාවකින් සහ එකතු කිරීමෙන් ගුණ කිරීමේ ප්‍රතිඵලයක් ලෙස එකම මානයක න්‍යාසයක් ලැබේ.

ශුන්‍ය න්‍යාසයක් යනු ශුන්‍ය වලින් සමන්විත න්‍යාසයකි. එය O ලෙස දැක්වේ. නිසැකවම, A +O = A, A -A = O සහ 0A = O.

අනුකෘතිය විය හැක මාරු කරන්න. මෙම මෙහෙයුම අතරතුර, අනුකෘතිය පෙරළනු ලැබේ, i.e. පේළි සහ තීරු මාරු කර ඇත. ප්‍රතිවර්තනය ප්‍රථමක, A" හෝ උපසිරසි A t මගින් දක්වනු ලැබේ. මේ අනුව, A = ( a ij , i = 1,..., අයි; j = 1,...,ජේ), පසුව A t = ( a ji , j = 1,...,ජේ; i = 1,..., අයි) උදාහරණ වශයෙන්

සහල්. 5 න්‍යාස මාරු කිරීම

(A t) t = A, (A + B) t = A t + B t බව පැහැදිලිය.

1.3 Matrix ගුණ කිරීම

Matrices විය හැක ගුණ කරන්න, නමුත් ඒවාට සුදුසු මානයන් තිබේ නම් පමණි. මෙය එසේ වන්නේ මන්දැයි අර්ථ දැක්වීමෙන් පැහැදිලි වනු ඇත. න්‍යාසයේ නිෂ්පාදිතය A, මානය අයි× කේ, සහ matrix B, මානය කේ× ජේ, matrix C, මානය ලෙස හැඳින්වේ අයි× ජේ, එහි මූලද්‍රව්‍ය සංඛ්‍යා වේ

මේ අනුව, AB නිෂ්පාදනය සඳහා වම් න්‍යාස A හි තීරු ගණන B දකුණු න්‍යාසයේ පේළි ගණනට සමාන වීම අවශ්‍ය වේ. matrix නිෂ්පාදනයක උදාහරණයක් -

Fig.6 න්‍යාසවල නිෂ්පාදිතය

න්‍යාස ගුණ කිරීමේ රීතිය පහත පරිදි සකස් කළ හැක. ඡේදනය වන ස්ථානයේ C අනුකෘතියේ මූලද්‍රව්‍යයක් සොයා ගැනීම සඳහා i-වන පේළිය සහ jවෙනි තීරුව ( c ij) මූලද්‍රව්‍යයෙන් මූලද්‍රව්‍ය ගුණ කළ යුතුය iපළමු න්‍යාසය A හි -වන පේළිය මත jදෙවන න්‍යාසය B හි තීරුව සහ සියලු ප්‍රතිඵල එකතු කරන්න. එබැවින් පෙන්වා ඇති උදාහරණයේ, තුන්වන පේළියේ සහ දෙවන තීරුවෙන් මූලද්‍රව්‍යයක් තුන්වන පේළියේ A සහ ​​දෙවන තීරුවේ B හි මූලද්‍රව්‍ය අනුව නිෂ්පාදනවල එකතුව ලෙස ලබා ගනී.

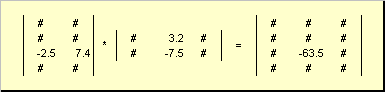
Fig.7 න්‍යාසවල ගුණිතයේ මූලද්‍රව්‍යය

න්‍යාසවල නිෂ්පාදිතය අනුපිළිවෙල මත රඳා පවතී, i.e. AB ≠ BA, අවම වශයෙන් මාන හේතු සඳහා. එය මාරු නොවන බව ඔවුහු පවසති. කෙසේ වෙතත්, න්‍යාසවල නිෂ්පාදිතය ආශ්‍රිත වේ. මෙයින් අදහස් කරන්නේ ABC = (AB)C = A(BC). ඊට අමතරව, එය ද බෙදා හරිනු ලැබේ, i.e. A (B +C) = AB + AC. පැහැදිලිවම AO = O.

1.4 හතරැස් matrices

න්‍යාස තීරු ගණන එහි පේළි ගණනට සමාන නම් ( අයි = J=N), එවිට එවැනි අනුකෘතියක් වර්ග ලෙස හැඳින්වේ. මෙම කොටසේදී අපි සලකා බලන්නේ එවැනි matrices පමණි. මෙම න්‍යාස අතර විශේෂ ගුණ ඇති න්‍යාස වෙන්කර හඳුනාගත හැකිය.

තනිකඩ matrix (I, සහ සමහර විට E) යනු න්‍යාසයකි, එහි සියලුම මූලද්‍රව්‍ය ශුන්‍යයට සමාන වේ, විකර්ණ ඒවා හැර, 1 ට සමාන වේ, i.e.

පැහැදිලිවම AI = IA = A.

අනුකෘතිය ලෙස හැඳින්වේ විකර්ණ, විකර්ණ හැර එහි සියලුම මූලද්‍රව්‍ය නම් ( a ii) ශුන්‍යයට සමාන වේ. උදාහරණ වශයෙන්

සහල්. 8 විකර්ණ අනුකෘතිය

Matrix A ඉහළ ලෙස හැඳින්වේ ත්රිකෝණාකාර, විකර්ණයට පහළින් පිහිටා ඇති එහි සියලුම මූලද්‍රව්‍ය ශුන්‍යයට සමාන නම්, i.e. a ij= 0, at i>j. උදාහරණ වශයෙන්

සහල්. 9 ඉහළ ත්රිකෝණාකාර අනුකෘතිය

පහළ ත්රිකෝණාකාර අනුකෘතිය සමාන ලෙස අර්ථ දක්වා ඇත.

Matrix A ලෙස හැඳින්වේ සමමිතික, A t = A නම් . වෙනත් විදිහකින් a ij = a ji. උදාහරණ වශයෙන්

සහල්. 10 සමමිතික අනුකෘතිය

Matrix A ලෙස හැඳින්වේ විකලාංග, නම්

A t A = AA t = I .

අනුකෘතිය ලෙස හැඳින්වේ සාමාන්යනම්

1.5 ලුහුබැඳීම සහ නිර්ණය කිරීම

ඊළඟවර්ග න්‍යාස A (Tr(A) හෝ Sp(A) මගින් දැක්වෙන්නේ එහි විකර්ණ මූලද්‍රව්‍යවල එකතුවයි,

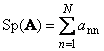
උදාහරණ වශයෙන්,

සහල්. 11 Matrix හෝඩුවාවක්

ඒක පැහැදිලියි

Sp(α A) = α Sp(A) සහ

Sp(A +B) = Sp(A)+ Sp(B).

ඒක පෙන්නන්න පුළුවන්

Sp(A) = Sp(A t), Sp(I) = එන්,

ඒ වගේම

Sp(AB) = Sp(BA).

හතරැස් න්‍යාසයක තවත් වැදගත් ලක්ෂණයක් වන්නේ එයයි නිර්ණායකය(det(A) මගින් දැක්වේ). සාමාන්‍ය නඩුවේ නිර්ණායකය තීරණය කිරීම තරමක් අපහසුය, එබැවින් අපි සරලම විකල්පය සමඟ ආරම්භ කරමු - මානයක A matrix (2 × 2). එතකොට

(3×3) න්‍යාසයක් සඳහා, නිර්ණායකය සමාන වේ

අනුකෘතිය සම්බන්ධයෙන් ( එන්× එන්) නිර්ණායකය 1·2·3· ... · එකතුව ලෙස ගණනය කෙරේ. එන්= එන්! නියමයන්, ඒ සෑම එකක්ම සමාන වේ

දර්ශක කේ 1 , කේ 2 ,..., කේ එන්හැකි සියලුම ඇණවුම් ප්‍රතිවර්තන ලෙස අර්ථ දක්වා ඇත ආර්කට්ටලයේ අංක (1, 2, ..., එන්) න්‍යාසයක නිර්ණායකය ගණනය කිරීම සංකීර්ණ ක්‍රියා පටිපාටියක් වන අතර එය ප්‍රායෝගිකව විශේෂ වැඩසටහන් භාවිතයෙන් සිදු කෙරේ. උදාහරණ වශයෙන්,

සහල්. 12 අනුකෘති නිර්ණය

අපි පැහැදිලි ගුණාංග පමණක් සටහන් කරමු:

det(I) = 1, det(A) = det(A t),

det(AB) = det(A)det(B).

1.6 දෛශික

න්‍යාසය සමන්විත වන්නේ එක් තීරුවකින් පමණක් නම් ( ජේ= 1), එවිට එවැනි වස්තුවක් ලෙස හැඳින්වේ දෛශිකය. වඩාත් නිවැරදිව, තීරු දෛශිකයකි. උදාහරණ වශයෙන්

උදාහරණයක් ලෙස, එක් පේළියකින් සමන්විත න්‍යාස සලකා බැලිය හැකිය

මෙම වස්තුව ද දෛශිකයකි, නමුත් පේළි දෛශිකය. දත්ත විශ්ලේෂණය කිරීමේදී, අප ගනුදෙනු කරන්නේ කුමන දෛශිකද යන්න තේරුම් ගැනීම වැදගත්ය - තීරු හෝ පේළි. එබැවින් එක් සාම්පලයක් සඳහා ගන්නා වර්ණාවලිය පේළි දෛශිකයක් ලෙස සැලකිය හැකිය. එවිට සියලුම සාම්පල සඳහා යම් තරංග ආයාමයක වර්ණාවලි තීව්‍රතා කට්ටලය තීරු දෛශිකයක් ලෙස සැලකිය යුතුය.

දෛශිකයක මානය යනු එහි මූලද්‍රව්‍ය ගණනයි.

ඕනෑම තීරු දෛශිකයක් මාරුවෙන් මාරුවට පේළි දෛශිකයක් බවට පත් කළ හැකි බව පැහැදිලිය, i.e.

දෛශිකයේ හැඩය නිශ්චිතව ප්‍රකාශ කර නැති නමුත් සරළව දෛශිකයක් යැයි කියන විට ඒවා තීරු දෛශිකයක් අදහස් කරයි. අපි ද මෙම රීතිය පිළිපදින්නෙමු. දෛශිකයක් කුඩා අකුරු, අවංක, තද අකුරකින් දැක්වේ. ශුන්‍ය දෛශිකයක් යනු දෛශිකයක් වන අතර එහි සියලුම මූලද්‍රව්‍ය ශුන්‍ය වේ. එය 0 ලෙස නම් කර ඇත.

1.7 දෛශික සමඟ සරලම මෙහෙයුම්

දෛශික න්‍යාස වලට සමාන ලෙස සංඛ්‍යා වලින් එකතු කර ගුණ කල හැක. උදාහරණ වශයෙන්,

සහල්. 13 දෛශික සමඟ මෙහෙයුම්

x සහ y දෛශික දෙකක් හැඳින්වේ colinear, එවැනි α අංකයක් තිබේ නම්

1.8 දෛශික නිෂ්පාදන

එකම මානයක දෛශික දෙකක් එන්ගුණ කළ හැක. දෛශික දෙකක් තිබිය යුතුය x = ( x 1 , x 2 ,...,x N) t සහ y = ( y 1 , y 2 ,...,y N) ටී. පේළියෙන් තීරු ගුණ කිරීමේ රීතියෙන් මඟ පෙන්වනු ලබන අතර, අපට ඒවායින් නිෂ්පාදන දෙකක් සෑදිය හැකිය: x t y සහ xy t. පළමු කාර්යය

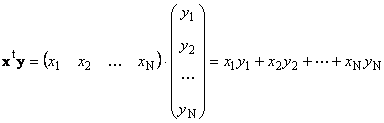
කියලා පරිමාණහෝ අභ්යන්තර. එහි ප්රතිඵලය සංඛ්යාවකි. (x ,y )= x t y යන අංකනය ද ඒ සඳහා භාවිතා වේ. උදාහරණ වශයෙන්,

සහල්. 14 අභ්‍යන්තර (අදිශ) නිෂ්පාදනය

දෙවන කෑල්ල

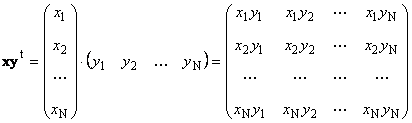
කියලා බාහිර. එහි ප්‍රතිඵලය මානයෙහි අනුකෘතියකි ( එන්× එන්) උදාහරණ වශයෙන්,

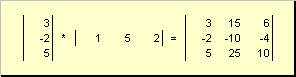
සහල්. 15 බාහිර වැඩ

අදිශ නිෂ්පාදන ශුන්‍ය වන දෛශික ලෙස හැඳින්වේ විකලාංග.

1.9 දෛශික සම්මතය

දෛශිකයක අදිශ ගුණිතය අදිශ වර්ග ලෙස හැඳින්වේ. මෙම අගය

චතුරස්රයක් නිර්වචනය කරයි දිගදෛශිකය x. දිග දැක්වීමට (එසේම හැඳින්වේ සම්මතය vector) අංකනය භාවිතා වේ

උදාහරණ වශයෙන්,

සහල්. 16 දෛශික සම්මතය

ඒකක දිග (||x || = 1) දෛශිකයක් සාමාන්‍යකරණය ලෙස හැඳින්වේ. ශුන්‍ය නොවන දෛශිකයක් (x ≠ 0) එහි දිගෙන් බෙදීමෙන් සාමාන්‍යකරණය කළ හැක, i.e. x = ||x || (x/ ||x ||) = ||x || ඊ. මෙහි e = x/ ||x || - සාමාන්‍යකරණය වූ දෛශිකය.

දෛශික සියල්ල සාමාන්‍යකරණය වී යුගල වශයෙන් විකලාංග නම් විකලාංග ලෙස හැඳින්වේ.

1.10 දෛශික අතර කෝණය

පරිමාණ නිෂ්පාදනය තීරණය කරයි සහ කෙළවරේ x සහ y දෛශික දෙකක් අතර φ

දෛශික විකලාංග නම්, cosφ = 0 සහ φ = π/2, සහ ඒවා colinear නම්, cosφ = 1 සහ φ = 0.

1.11. අනුකෘතියක දෛශික නිරූපණය

ප්‍රමාණයෙන් එක් එක් න්‍යාස A අයි× ජේදෛශික කට්ටලයක් ලෙස දැක්විය හැක

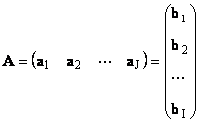
මෙහි එක් එක් දෛශිකය a jවේ j th තීරුව, සහ පේළි දෛශිකය b iවේ iන්‍යාසයේ A පේළිය

1.12 රේඛීයව යැපෙන දෛශික

එකම මානයක දෛශික ( එන්) න්‍යාස මෙන් සංඛ්‍යාවකින් එකතු කර ගුණ කළ හැක. ප්රතිඵලය එකම මානයක දෛශිකයක් වනු ඇත. එකම මානයක දෛශික කිහිපයක් x 1, x 2,...,x K සහ එම සංඛ්‍යා α α 1, α 2,...,α වේවා කේ. දෛශිකය

y = α 1 x 1 + α 2 x 2 +...+ α කේ x කේ

කියලා රේඛීය සංයෝජනයදෛශික x කේ .

එවැනි ශුන්‍ය නොවන සංඛ්‍යා තිබේ නම් α කේ ≠ 0, කේ = 1,..., කේඑනම් y = 0, එවිට එවැනි දෛශික x කට්ටලයක් කේකියලා රේඛීයව රඳා පවතී. එසේ නොමැති නම්, දෛශික රේඛීය ස්වාධීන ලෙස හැඳින්වේ. උදාහරණයක් ලෙස, දෛශික x 1 = (2, 2) t සහ x 2 = (−1, -1) t රේඛීයව රඳා පවතී, මන්ද x 1 +2x 2 = 0

1.13 Matrix ශ්‍රේණිය

කට්ටලයක් සලකා බලන්න කේදෛශික x 1 , x 2 ,...,x කේමානයන් එන්. මෙම දෛශික පද්ධතියේ ශ්‍රේණිය රේඛීය ස්වාධීන දෛශික උපරිම සංඛ්‍යාවයි. උදාහරණයක් ලෙස කට්ටලය තුළ

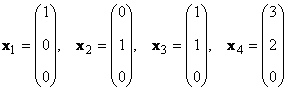
ඇත්තේ රේඛීය ස්වාධීන දෛශික දෙකක් පමණි, උදාහරණයක් ලෙස x 1 සහ x 2, එබැවින් එහි ශ්‍රේණිය 2 වේ.

පැහැදිලිවම, කට්ටලයක ඒවායේ මානයට වඩා දෛශික තිබේ නම් ( කේ>එන්), එවිට ඒවා අනිවාර්යයෙන්ම රේඛීයව රඳා පවතී.

Matrix ශ්‍රේණිය(ශ්‍රේණිගත කිරීම (A)) යනු එය සමන්විත වන දෛශික පද්ධතියේ ශ්‍රේණියයි. ඕනෑම න්‍යාසයක් ආකාර දෙකකින් (තීරු හෝ පේළි දෛශික) නිරූපණය කළ හැකි වුවද, මෙය ශ්‍රේණිගත අගයට බලපාන්නේ නැත, මන්ද

1.14. ප්රතිලෝම න්යාසය

A වර්ග න්‍යාසයකට අනන්‍ය වූවක් තිබේ නම් එය ඒකීය නොවන ලෙස හැඳින්වේ ආපසු හැරවීම matrix A -1 කොන්දේසි අනුව තීරණය වේ

AA -1 = A -1 A = I .

සියලු න්‍යාස සඳහා ප්‍රතිලෝම න්‍යාසය නොපවතී. පරිහානියට පත් නොවීම සඳහා අවශ්ය සහ ප්රමාණවත් කොන්දේසියකි

det(A) ≠ 0 හෝ ශ්‍රේණිය(A) = එන්.

Matrix inversion යනු විශේෂ වැඩසටහන් ඇති සංකීර්ණ ක්‍රියා පටිපාටියකි. උදාහරණ වශයෙන්,

සහල්. 17 Matrix ප්‍රතිලෝම

අපි සරලම අවස්ථාව සඳහා සූත්‍ර ඉදිරිපත් කරමු - 2×2 න්‍යාසයක්

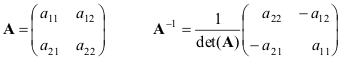
A සහ B න්‍යාස ඒකීය නොවන නම්, එසේ නම්

(AB) -1 = B -1 A -1 .

1.15 ව්යාජ ප්රතිලෝම අනුකෘතිය

A න්‍යාසය ඒකීය නම් සහ ප්‍රතිලෝම න්‍යාසය නොපවතී නම්, සමහර අවස්ථාවලදී ඔබට භාවිතා කළ හැක ව්යාජ ප්රතිලෝමන්‍යාසය, A+ න්‍යාසයක් ලෙස අර්ථ දක්වා ඇත

AA + A = A.

ව්‍යාජ න්‍යාසය එකම එක නොවන අතර එහි ආකෘතිය ඉදිකිරීම් ක්‍රමය මත රඳා පවතී. උදාහරණයක් ලෙස, සෘජුකෝණාස්රාකාර අනුකෘතියක් සඳහා ඔබට Moore-Penrose ක්රමය භාවිතා කළ හැකිය.

තීරු ගණන පේළි ගණනට වඩා අඩු නම්, එසේ නම්

A + =(A t A ) -1 A ටී

උදාහරණ වශයෙන්,

සහල්. 17a අනුකෘතියක ව්‍යාජ ප්‍රතිලෝම

තීරු ගණන පේළි ගණනට වඩා වැඩි නම්, එසේ නම්

A + =A t (AA t) -1

1.16. දෛශිකයක් අනුකෘතියකින් ගුණ කිරීම

දෛශික x සුදුසු මානයක A matrix එකකින් ගුණ කළ හැක. මෙම අවස්ථාවෙහිදී, තීරු දෛශිකය දකුණු පොරව මත ගුණ කරනු ලැබේ, පේළි දෛශිකය වම් x t A මත ගුණ කරනු ලැබේ. දෛශික මානය නම් ජේ, සහ matrix මානය අයි× ජේඑවිට ප්රතිඵලය මානයක දෛශිකයක් වනු ඇත අයි. උදාහරණ වශයෙන්,

සහල්. 18 දෛශිකයක් අනුකෘතියකින් ගුණ කිරීම

න්‍යාසය A හතරැස් නම් ( අයි× අයි), එවිට දෛශිකය y = Ax ට සමාන මානයක් ඇත. ඒක පැහැදිලියි

A (α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

එබැවින් න්‍යාස දෛශිකවල රේඛීය පරිවර්තන ලෙස සැලකිය හැකිය. විශේෂයෙන්ම Ix = x, Ox = 0.

2. අමතර තොරතුරු 2.1. රේඛීය සමීකරණ පද්ධති

A ප්‍රමාණයේ න්‍යාසයක් වේවා අයි× ජේ, සහ b යනු මාන දෛශිකයයි ජේ. සමීකරණය සලකා බලන්න

Ax = b

දෛශිකයට සාපේක්ෂව x, මානය අයි. අත්යවශ්යයෙන්ම, එය පද්ධතියකි අයිසමඟ රේඛීය සමීකරණ ජේනොදන්නා x 1 ,...,x ජේ. විසඳුමක් පවතින්නේ නම් සහ නම් පමණි

rank(A) = rank(B) = ආර්,

මෙහි B යනු වර්ධක මාන න්‍යාසයයි අයි×( J+1), b, B = (A b) තීරුවකින් අනුපූරක A න්‍යාසයකින් සමන්විත වේ. එසේ නොමැති නම්, සමීකරණ නොගැලපේ.

නම් ආර් = අයි = ජේ, එවිට විසඳුම අද්විතීයයි

x = A -1 b .

නම් ආර් < අයි, එවිට රේඛීය සංයෝජනයක් හරහා ප්‍රකාශ කළ හැකි විවිධ විසඳුම් තිබේ ජේ−ආර්දෛශික. සමජාතීය සමීකරණ පද්ධතිය Ax = 0 වර්ග න්‍යාසය A ( එන්× එන්) සුළු නොවන විසඳුමක් (x ≠ 0) තිබේ නම් සහ det(A) = 0 නම් පමණි. ආර්= ශ්‍රේණිය(A) 0.

ඒ හා සමානව අර්ථ දක්වා ඇත සෘණ(x t Ax< 0), සෘණ නොවන(x t Ax ≥ 0) සහ සෘණ(x t Ax ≤ 0) ඇතැම් matrices.

2.4 Cholesky වියෝජනය

සමමිතික න්‍යාසයක් A ධන නිශ්චිත නම්, ඒ සඳහා ධන මූලද්‍රව්‍ය සහිත U අද්විතීය ත්‍රිකෝණාකාර න්‍යාසයක් ඇත.

A = U t U .

උදාහරණ වශයෙන්,

සහල්. 19 Cholesky වියෝජනය

2.5 ධ්රැවීය වියෝජනය

A මානයෙහි ඒකීය නොවන වර්ග න්‍යාසයක් වේවා එන්× එන්. එවිට අද්විතීය එකක් ඇත ධ්රැවීයකාර්ය සාධනය

A = SR,

මෙහි S යනු සෘණ නොවන සමමිතික න්‍යාසයක් වන අතර R යනු විකලාංග න්‍යාසයකි. න්‍යාස S සහ R පැහැදිලිව අර්ථ දැක්විය හැක:

S 2 = AA t හෝ S = (AA t) ½ සහ R = S -1 A = (AA t) -½ A .

උදාහරණ වශයෙන්,

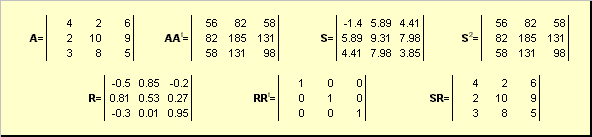
සහල්. 20 ධ්රැවීය වියෝජනය

A අනුකෘතිය ඒකීය නම්, වියෝජනය අද්විතීය නොවේ - එනම්: S තවමත් එකකි, නමුත් බොහෝ R තිබිය හැක. ධ්‍රැවීය විසංයෝජනය මගින් සංකෝචනය/දිගුව S සහ භ්‍රමණය R හි එකතුවක් ලෙස matrix A නියෝජනය කරයි.

2.6 Eigenvectors සහ Eigenvalues

A හතරැස් න්‍යාසයක් වේවා. දෛශිකය v ලෙස හැඳින්වේ eigenvector matrix A නම්

Av = λv,

එහිදී λ අංකය හැඳින්වේ eigenvalue matrices A. මේ අනුව, න්‍යාසය A දෛශික v මත සිදු කරන පරිවර්තනය සංගුණකය λ සමඟ සරල දිගු කිරීමකට හෝ සම්පීඩනයකට අඩු වේ. eigenvector නියත α ≠ 0 මගින් ගුණ කිරීම දක්වා තීරණය වේ, i.e. v යනු අයිගන් දෛශිකයක් නම්, αv ද අයිගන් දෛශිකයකි.

2.7 Eigenvalues

A න්‍යාසයට මානය ඇත ( එන්× එන්) වඩා වැඩි විය නොහැක එන් eigenvalues. ඔවුන් සෑහීමකට පත්වේ ලක්ෂණ සමීකරණය

det(A - λI) = 0,

වීජීය සමීකරණයක් වන එන්-වන නියෝගය. විශේෂයෙන්ම, 2×2 න්‍යාසයක් සඳහා ලාක්ෂණික සමීකරණයේ ස්වරූපය ඇත

උදාහරණ වශයෙන්,

සහල්. 21 Eigenvalues

eigenvalues ​​කට්ටලය λ 1 ,..., λ එන් matrix A ලෙස හැඳින්වේ වර්ණාවලියඒ.

වර්ණාවලියට විවිධ ගුණ ඇත. විශේෂයෙන්ම

det(A) = λ 1 ×...×λ එන්, Sp(A) = λ 1 +...+λ එන්.

අත්තනෝමතික න්‍යාසයක eigenvalues ​​සංකීර්ණ සංඛ්‍යා විය හැකි නමුත් න්‍යාසය සමමිතික (A t = A) නම් එහි eigenvalues ​​සැබෑ වේ.

2.8 Eigenvectors

A න්‍යාසයට මානය ඇත ( එන්× එන්) වඩා වැඩි විය නොහැක එන් eigenvectors, ඒ සෑම එකක්ම තමන්ගේම eigenvalue වලට අනුරූප වේ. අයිගන් දෛශිකය තීරණය කිරීම සඳහා v nසමජාතීය සමීකරණ පද්ධතියක් විසඳීමට අවශ්ය වේ

(A - λ n I) v n = 0 .

det(A - λ) නිසා එයට සුළු නොවන විසඳුමක් ඇත n I) = 0.

උදාහරණ වශයෙන්,

සහල්. 22 අයිගන් දෛශික

සමමිතික අනුකෘතියක අයිගන් දෛශික විකලාංග වේ.

හතරැස් න්‍යාසයක අයිගන් දෛශිකයක් යනු, දී ඇති න්‍යාසයකින් ගුණ කළ විට, ඛණ්ඩක දෛශිකයක් ඇති වන එකකි. සරල වචන වලින් කිවහොත්, න්‍යාසයක් අයිගන් දෛශිකයකින් ගුණ කළ විට, දෙවැන්න එලෙසම පවතින නමුත් නිශ්චිත සංඛ්‍යාවකින් ගුණ කරනු ලැබේ.

අර්ථ දැක්වීම

අයිගන් දෛශිකයක් යනු ශුන්‍ය නොවන දෛශික V වන අතර, එය M වර්ග න්‍යාසයකින් ගුණ කළ විට එය යම් සංඛ්‍යාවක් λ කින් වැඩි වේ. වීජීය අංකනයේදී එය පෙනෙන්නේ:

M × V = λ × V,

මෙහි λ යනු M න්‍යාසයේ eigenvalue වේ.

අපි සංඛ්‍යාත්මක උදාහරණයක් බලමු. පටිගත කිරීමේ පහසුව සඳහා, න්‍යාසයේ සංඛ්‍යා අර්ධ කෝලයකින් වෙන් කරනු ලැබේ. අපි matrix එකක් ගනිමු:

  • M = 0; 4;
  • 6; 10.

තීරු දෛශිකයකින් එය ගුණ කරමු:

  • V = -2;

න්‍යාසයක් තීරු දෛශිකයකින් ගුණ කළ විට අපට තීරු දෛශිකයක් ද ලැබේ. දැඩි ගණිතමය භාෂාවෙන්, තීරු දෛශිකයකින් 2 × 2 න්‍යාසයක් ගුණ කිරීමේ සූත්‍රය මේ ආකාරයෙන් පෙනෙනු ඇත:

  • M × V = M11 × V11 + M12 × V21;
  • M21 × V11 + M22 × V21.

M11 යනු පළමු පේළියේ සහ පළමු තීරුවේ පිහිටා ඇති න්‍යාසයේ M මූලද්‍රව්‍යය වන අතර M22 යනු දෙවන පේළියේ සහ දෙවන තීරුවේ පිහිටා ඇති මූලද්‍රව්‍යය වේ. අපගේ න්‍යාසය සඳහා, මෙම මූලද්‍රව්‍ය M11 = 0, M12 = 4, M21 = 6, M22 10 ට සමාන වේ. තීරු දෛශිකයක් සඳහා, මෙම අගයන් V11 = –2, V21 = 1 ට සමාන වේ. මෙම සූත්‍රය අනුව, දෛශිකයකින් වර්ග න්‍යාසයක ගුණිතයේ පහත ප්‍රතිඵලය අපට ලැබේ:

  • M × V = 0 × (-2) + (4) × (1) = 4;
  • 6 × (-2) + 10 × (1) = -2.

පහසුව සඳහා, තීරු දෛශිකය පේළියකට ලියමු. එබැවින්, අපි දෛශිකයෙන් වර්ග න්‍යාසය ගුණ කළෙමු (-2; 1), එහි ප්‍රතිඵලයක් ලෙස දෛශිකය (4; -2). පැහැදිලිවම, මෙය λ = -2 න් ගුණ කළ එකම දෛශිකය වේ. මෙම නඩුවේ Lambda අනුකෘතියේ eigenvalue දක්වයි.

න්‍යාසයක අයිගන් දෛශිකයක් යනු collinear දෛශිකයකි, එනම් න්‍යාසයකින් ගුණ කළ විට අවකාශයේ පිහිටීම වෙනස් නොකරන වස්තුවකි. දෛශික වීජ ගණිතයේ සහසම්බන්ධතා සංකල්පය ජ්‍යාමිතියේ සමාන්තරතා පදයට සමාන වේ. ජ්‍යාමිතික විග්‍රහයක දී, collinear දෛශික යනු විවිධ දිගින් යුත් සමාන්තර දිශානුගත කොටස් වේ. යුක්ලීඩ් යුගයේ සිටම, එක් පේළියකට සමාන්තර රේඛා අනන්ත සංඛ්‍යාවක් ඇති බව අපි දනිමු, එබැවින් සෑම න්‍යාසයකටම අනන්ත අයිගන් දෛශික සංඛ්‍යාවක් ඇතැයි උපකල්පනය කිරීම තර්කානුකූල ය.

පෙර උදාහරණයෙන් පැහැදිලි වන්නේ අයිගන් දෛශික (-8; 4), සහ (16; -8), සහ (32, -16) විය හැකි බවයි. මේ සියල්ල λ = -2 eigenvalue ට අනුරූප වන collinear දෛශික වේ. මෙම දෛශික මගින් මුල් න්‍යාසය ගුණ කරන විට, අපි තවමත් මුල් න්‍යාසයට වඩා 2 ගුණයකින් වෙනස් වන දෛශිකයකින් අවසන් වනු ඇත. අයිගන් දෛශිකයක් සොයා ගැනීමේ ගැටළු විසඳීමේදී රේඛීයව ස්වාධීන දෛශික වස්තූන් පමණක් සොයා ගැනීම අවශ්‍ය වන්නේ එබැවිනි. බොහෝ විට, n × n න්‍යාසයක් සඳහා, අයිගන් දෛශික n සංඛ්‍යාවක් ඇත. අපගේ කැල්කියුලේටරය නිර්මාණය කර ඇත්තේ දෙවන පෙළ වර්ග න්‍යාස විශ්ලේෂණය සඳහා වන අතර, එම නිසා සෑම විටම පාහේ ප්‍රතිඵලය eigenvectors දෙකක් සොයා ගනු ඇත, ඒවා සමපාත වන අවස්ථා හැර.

ඉහත උදාහරණයේ දී, අපි මුල් අනුකෘතියේ අයිගන් දෛශිකය කල්තියා දැන සිටි අතර ලැම්ඩා අංකය පැහැදිලිව තීරණය කළෙමු. කෙසේ වෙතත්, ප්රායෝගිකව, සෑම දෙයක්ම අනෙක් අතට සිදු වේ: eigenvalues ​​මුලින්ම සොයා ගන්නා අතර පසුව පමණක් eigenvectors.

විසඳුම් ඇල්ගොරිතම

අපි නැවතත් මුල් matrix M දෙස බලා එහි eigenvectors දෙකම සොයා ගැනීමට උත්සාහ කරමු. එබැවින් අනුකෘතිය පෙනෙන්නේ:

  • M = 0; 4;
  • 6; 10.

පළමුව අපි eigenvalue λ තීරණය කළ යුතුය, ඒ සඳහා පහත න්‍යාසයේ නිර්ණායකය ගණනය කිරීම අවශ්‍ය වේ:

  • (0 - λ); 4;
  • 6; (10 - λ).

මෙම න්‍යාසය ප්‍රධාන විකර්ණයේ ඇති මූලද්‍රව්‍ය වලින් නොදන්නා λ අඩු කිරීමෙන් ලබා ගනී. නිර්ණායකය සම්මත සූත්රය භාවිතයෙන් තීරණය වේ:

  • detA = M11 × M21 - M12 × M22
  • detA = (0 - λ) × (10 - λ) - 24

අපගේ දෛශිකය ශුන්‍ය නොවිය යුතු බැවින්, අපි ලැබෙන සමීකරණය රේඛීයව යැපෙන ලෙස පිළිගෙන අපගේ නිර්ණායක detA ශුන්‍යයට සමාන කරමු.

(0 - λ) × (10 - λ) - 24 = 0

අපි වරහන් විවෘත කර අනුකෘතියේ ලාක්ෂණික සමීකරණය ලබා ගනිමු:

λ 2 - 10λ - 24 = 0

මෙය වෙනස් කොට සැලකීමක් භාවිතයෙන් විසඳිය යුතු සම්මත චතුරස්‍ර සමීකරණයකි.

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

discriminant හි මූලය sqrt(D) = 14, එබැවින් λ1 = -2, λ2 = 12. දැන් සෑම lambda අගයක් සඳහාම අපි eigenvector සොයා ගත යුතුය. අපි λ = -2 සඳහා පද්ධති සංගුණක ප්රකාශ කරමු.

  • M - λ × E = 2; 4;
  • 6; 12.

මෙම සූත්‍රයේ E යනු අනන්‍යතා අනුකෘතියයි. ලැබෙන අනුකෘතිය මත පදනම්ව, අපි රේඛීය සමීකරණ පද්ධතියක් නිර්මාණය කරමු:

2x + 4y = 6x + 12y,

මෙහි x සහ y යනු eigenvector මූලද්‍රව්‍ය වේ.

වම් පස ඇති සියලුම X සහ දකුණු පස ඇති සියලුම Y එකතු කරමු. පැහැදිලිවම - 4x = 8y. ප්‍රකාශනය - 4 න් බෙදා x = –2y ලබා ගන්න. දැන් අපට න්‍යාසයේ පළමු අයිගන් දෛශිකය තීරණය කළ හැකි අතර, නොදන්නා අගයන්හි ඕනෑම අගයක් ගනිමින් (රේඛීයව යැපෙන අයිගන් දෛශිකවල අනන්තය මතක තබා ගන්න). අපි y = 1, පසුව x = –2 ගනිමු. එබැවින්, පළමු eigenvector V1 = (-2; 1) ලෙස පෙනේ. ලිපියේ ආරම්භය වෙත ආපසු යන්න. අයිගන් දෛශික සංකල්පය නිරූපණය කිරීම සඳහා අපි අනුකෘතිය ගුණ කළේ මෙම දෛශික වස්තුවයි.

දැන් අපි λ = 12 සඳහා අයිගන් දෛශිකය සොයා ගනිමු.

  • M - λ × E = -12; 4
  • 6; -2.

රේඛීය සමීකරණ පද්ධතියම නිර්මාණය කරමු;

  • -12x + 4y = 6x - 2y
  • -18x = -6y
  • 3x = y.

දැන් අපි ගන්නේ x = 1, ඒ නිසා y = 3. මේ අනුව, දෙවන eigenvector V2 = (1; 3) ලෙස පෙනේ. ලබා දී ඇති දෛශිකයකින් මුල් න්‍යාසය ගුණ කරන විට, ප්‍රතිඵලය සෑම විටම එකම දෛශිකය 12 න් ගුණ කරනු ලැබේ. විසඳුම ඇල්ගොරිතම අවසන් වන්නේ මෙතැනිනි. න්‍යාසයක අයිගන් දෛශිකය අතින් නිර්ණය කරන්නේ කෙසේදැයි දැන් ඔබ දන්නවා.

  • නිර්ණායක;
  • හෝඩුවාවක්, එනම් ප්‍රධාන විකර්ණයේ ඇති මූලද්‍රව්‍යවල එකතුව;
  • ශ්‍රේණිය, එනම් රේඛීය ස්වාධීන පේළි/තීරු උපරිම සංඛ්‍යාව.

ඉහත ඇල්ගොරිතමයට අනුව වැඩසටහන ක්රියාත්මක වන අතර, හැකිතාක් දුරට විසඳුම් ක්රියාවලිය අඩු කරයි. වැඩසටහනේ lambda "c" අක්ෂරයෙන් නම් කර ඇති බව පෙන්වා දීම වැදගත්ය. අපි සංඛ්‍යාත්මක උදාහරණයක් බලමු.

වැඩසටහන ක්රියාත්මක වන ආකාරය පිළිබඳ උදාහරණයක්

පහත න්‍යාසය සඳහා අයිගන් දෛශික තීරණය කිරීමට උත්සාහ කරමු:

  • M = 5; 13;
  • 4; 14.

අපි මෙම අගයන් කැල්කියුලේටරයේ සෛල තුළට ඇතුළු කර පිළිතුර පහත ආකාරයෙන් ලබා ගනිමු:

  • Matrix ශ්‍රේණිය: 2;
  • අනුකෘති නිර්ණය: 18;
  • අනුකෘති හෝඩුවාව: 19;
  • අයිගන් දෛශිකයේ ගණනය කිරීම: c 2 - 19.00c + 18.00 (ලාක්ෂණික සමීකරණය);
  • Eigenvector ගණනය: 18 (පළමු lambda අගය);
  • Eigenvector ගණනය: 1 (දෙවන lambda අගය);
  • දෛශික 1 සඳහා සමීකරණ පද්ධතිය: -13x1 + 13y1 = 4x1 - 4y1;
  • දෛශික 2 සඳහා සමීකරණ පද්ධතිය: 4x1 + 13y1 = 4x1 + 13y1;
  • Eigenvector 1: (1; 1);
  • Eigenvector 2: (-3.25; 1).

මේ අනුව, අපි රේඛීය ස්වාධීන අයිගන් දෛශික දෙකක් ලබා ගත්තෙමු.

නිගමනය

රේඛීය වීජ ගණිතය සහ විශ්ලේෂණාත්මක ජ්‍යාමිතිය ඕනෑම නවක ඉංජිනේරු සිසුවෙකු සඳහා සම්මත විෂයයන් වේ. දෛශික සහ න්‍යාස විශාල සංඛ්‍යාවක් භයානක වන අතර, එවැනි අපහසු ගණනය කිරීම් වලදී වැරදි සිදු කිරීම පහසුය. අපගේ වැඩසටහන සිසුන්ට ඔවුන්ගේ ගණනය කිරීම් පරීක්ෂා කිරීමට හෝ අයිගන් දෛශිකයක් සොයා ගැනීමේ ගැටලුව ස්වයංක්‍රීයව විසඳා ගැනීමට ඉඩ සලසයි. අපගේ නාමාවලියෙහි වෙනත් රේඛීය වීජ ගණිත ගණක යන්ත්‍ර තිබේ.

www.site ඔබට සොයා ගැනීමට ඉඩ සලසයි. වෙබ් අඩවිය ගණනය කිරීම සිදු කරයි. තත්පර කිහිපයකින් සේවාදායකය නිවැරදි විසඳුම ලබා දෙනු ඇත. න්‍යාසය සඳහා ලාක්ෂණික සමීකරණය න්‍යාස න්‍යාසයේ නිර්ණායකය ගණනය කිරීමේ රීතියට අනුව සොයාගත් වීජීය ප්‍රකාශනයක් වන අතර ප්‍රධාන විකර්ණය විකර්ණ මූලද්‍රව්‍යවල සහ විචල්‍යයේ අගයන්හි වෙනස වේ. සබැඳි න්‍යාසයක් සඳහා ලාක්ෂණික සමීකරණය ගණනය කිරීමේදී, න්‍යාසයේ සෑම මූලද්‍රව්‍යයක්ම අනුකෘතියේ අනෙකුත් මූලද්‍රව්‍ය සමඟ ගුණ කරනු ලැබේ. ඔබට එය මාර්ගගතව සොයා ගත හැක්කේ වර්ග අනුකෘතියක් සඳහා පමණි. ඔන්ලයින් න්‍යාසයක් සඳහා ලාක්ෂණික සමීකරණය සෙවීමේ ක්‍රියාකාරිත්වය න්‍යාසයේ නිර්ණායකය සොයා ගැනීමේ ප්‍රතිඵලයක් ලෙස න්‍යාස මූලද්‍රව්‍යවල ගුණිතයේ වීජීය එකතුව ගණනය කිරීම දක්වා අඩු කරනු ලබන්නේ අන්තර්ජාලය සඳහා ලාක්ෂණික සමීකරණය තීරණය කිරීමේ අරමුණින් පමණි. matrix. මෙම මෙහෙයුම matrix න්‍යායේ විශේෂ ස්ථානයක් ගනී; එය මූලයන් භාවිතා කරමින් eigenvalues ​​සහ vectors සොයා ගැනීමට ඔබට ඉඩ සලසයි. න්‍යාසයක් සඳහා ලාක්ෂණික සමීකරණය මාර්ගගතව සෙවීමේ කාර්යය සමන්විත වන්නේ න්‍යාසයේ මූලද්‍රව්‍ය ගුණ කිරීම සහ යම් රීතියකට අනුව මෙම නිෂ්පාදන සාරාංශ කිරීමයි. www.site ලබා දී ඇති මානයක න්‍යාසයක් සඳහා ලාක්ෂණික සමීකරණය මාර්ගගතව සොයා ගනී. දී ඇති මානයක් සඳහා සබැඳි න්‍යාසයක් සඳහා ලාක්ෂණික සමීකරණය ගණනය කිරීම යනු න්‍යාසයක නිර්ණායකය ගණනය කිරීමේ රීතියට අනුව සොයා ගන්නා සංඛ්‍යාත්මක හෝ සංකේතාත්මක සංගුණක සහිත බහුපදයක් සොයා ගැනීමයි - න්‍යාසයේ අනුරූප මූලද්‍රව්‍යවල නිෂ්පාදන එකතුව ලෙස, සඳහා පමණි. න්‍යාසය සඳහා ලාක්ෂණික සමීකරණය මාර්ගගතව තීරණය කිරීමේ අරමුණ. න්‍යාසය සඳහා ලාක්ෂණික සමීකරණයේ නිර්වචනයක් ලෙස වර්ග න්‍යාසයක් සඳහා විචල්‍යයක් සම්බන්ධයෙන් බහුපදයක් සොයා ගැනීම න්‍යාස න්‍යායේ පොදු වේ. ඔන්ලයින් න්‍යාසයක් සඳහා බහුපද ලාක්ෂණික සමීකරණයේ මූලයන්ගේ අගය න්‍යාසය සඳහා අයිගන් දෛශික සහ අයිගන් අගයන් තීරණය කිරීමට භාවිතා කරයි. තවද, න්‍යාසයේ නිර්ණායකය ශුන්‍යයට සමාන නම්, ප්‍රතිලෝම න්‍යාසය මෙන් නොව න්‍යාසයේ ලාක්ෂණික සමීකරණය තවමත් පවතිනු ඇත. අනුකෘතියක් සඳහා ලාක්ෂණික සමීකරණය ගණනය කිරීමට හෝ න්‍යාස කිහිපයක් සඳහා ලාක්ෂණික සමීකරණ එකවර සොයා ගැනීමට, ඔබ බොහෝ කාලයක් හා වෑයමක් දැරීමට සිදු වන අතර, අපගේ සේවාදායකය තත්පර කිහිපයකින් න්‍යාසයක් සඳහා වන ලාක්ෂණික සමීකරණය අන්තර්ජාලය හරහා සොයා ගනු ඇත. මෙම අවස්ථාවෙහිදී, සබැඳි න්‍යාසයක් සඳහා ලාක්ෂණික සමීකරණය සෙවීමට පිළිතුර නිවැරදි සහ ප්‍රමාණවත් නිරවද්‍යතාවයකින් යුක්ත වනු ඇත, සබැඳි න්‍යාසයක් සඳහා ලාක්ෂණික සමීකරණය සොයා ගැනීමේදී සංඛ්‍යා අතාර්කික වුවද. www.site වෙබ් අඩවියේ, න්‍යාස මූලද්‍රව්‍යවල සංකේතාත්මක ඇතුළත් කිරීම් වලට අවසර ඇත, එනම්, සබැඳි න්‍යාසයක ලාක්ෂණික සමීකරණය ගණනය කිරීමේදී සබැඳි න්‍යාසයක් සඳහා වන ලාක්ෂණික සමීකරණය සාමාන්‍ය සංකේතාත්මක ස්වරූපයෙන් නිරූපණය කළ හැකිය. www.site වෙබ් අඩවිය භාවිතා කරමින් අන්තර්ජාලය හරහා න්‍යාසයක් සඳහා ලාක්ෂණික සමීකරණය සෙවීමේ ගැටලුව විසඳීමේදී ලබාගත් පිළිතුර පරීක්ෂා කිරීම ප්‍රයෝජනවත් වේ. බහුපදයක් ගණනය කිරීමේ මෙහෙයුම සිදු කරන විට - න්‍යාසයක ලාක්ෂණික සමීකරණය, මෙම ගැටළුව විසඳීමේදී ඔබ ප්‍රවේශම් විය යුතු අතර අතිශයින්ම අවධානය යොමු කළ යුතුය. අනෙක් අතට, අන්තර්ජාලයේ අනුකෘතියක ලාක්ෂණික සමීකරණයේ මාතෘකාව පිළිබඳ ඔබේ විසඳුම පරීක්ෂා කිරීමට අපගේ වෙබ් අඩවිය ඔබට උපකාර කරනු ඇත. විසඳන ලද ගැටළු පිළිබඳ දිගු චෙක්පත් සඳහා ඔබට කාලය නොමැති නම්, අන්තර්ජාලය හරහා අනුකෘතියක් සඳහා ලාක්ෂණික සමීකරණය සොයා ගැනීම සහ ගණනය කිරීමේදී www.site නිසැකවම පහසු මෙවලමක් වනු ඇත.

වෙබ් අඩවියකට ගණිතමය සූත්‍ර ඇතුළත් කරන්නේ කෙසේද?

ඔබට කවදා හෝ වෙබ් පිටුවකට ගණිතමය සූත්‍ර එකක් හෝ දෙකක් එක් කිරීමට අවශ්‍ය නම්, මෙය කිරීමට ඇති පහසුම ක්‍රමය ලිපියේ විස්තර කර ඇති පරිදි වේ: ගණිතමය සූත්‍ර පහසුවෙන් වුල්ෆ්‍රම් ඇල්ෆා විසින් ස්වයංක්‍රීයව ජනනය කරන පින්තූර ආකාරයෙන් වෙබ් අඩවියට ඇතුළු කරනු ලැබේ. . සරලත්වයට අමතරව, මෙම විශ්වීය ක්රමය සෙවුම් යන්ත්රවල වෙබ් අඩවියේ දෘශ්යතාව වැඩිදියුණු කිරීමට උපකාරී වනු ඇත. එය දිගු කාලයක් තිස්සේ වැඩ කර ඇත (සහ, මම හිතන්නේ, සදහටම වැඩ කරනු ඇත), නමුත් දැනටමත් සදාචාරාත්මකව යල්පැන ඇත.

ඔබ නිතිපතා ඔබේ වෙබ් අඩවියේ ගණිතමය සූත්‍ර භාවිතා කරන්නේ නම්, මම ඔබට නිර්දේශ කරන්නේ MathJax - MathML, LaTeX හෝ ASCIIMathML සලකුණු භාවිතා කර වෙබ් බ්‍රව්සර්වල ගණිතමය අංකනය පෙන්වන විශේෂ JavaScript පුස්තකාලයකි.

MathJax භාවිතා කිරීම ආරම්භ කිරීමට ක්‍රම දෙකක් තිබේ: (1) සරල කේතයක් භාවිතයෙන්, ඔබට ඉක්මනින් MathJax ස්ක්‍රිප්ට් එකක් ඔබේ වෙබ් අඩවියට සම්බන්ධ කළ හැක, එය නිවැරදි වේලාවට දුරස්ථ සේවාදායකයකින් ස්වයංක්‍රීයව පූරණය වේ (සේවාදායක ලැයිස්තුව); (2) MathJax ස්ක්‍රිප්ට් එක දුරස්ථ සේවාදායකයකින් ඔබගේ සේවාදායකයට බාගත කර එය ඔබගේ අඩවියේ සියලුම පිටු වෙත සම්බන්ධ කරන්න. දෙවන ක්‍රමය - වඩාත් සංකීර්ණ සහ කාලය ගතවන - ඔබගේ වෙබ් අඩවියේ පිටු පූරණය වීම වේගවත් කරනු ඇති අතර, යම් හේතුවක් නිසා මව් MathJax සේවාදායකය තාවකාලිකව ලබා ගත නොහැකි වුවහොත්, මෙය ඔබගේම වෙබ් අඩවියට කිසිදු ආකාරයකින් බලපාන්නේ නැත. මෙම වාසි තිබියදීත්, මම පළමු ක්රමය තෝරා ගත්තේ එය සරල, වේගවත් හා තාක්ෂණික කුසලතා අවශ්ය නොවේ. මගේ ආදර්ශය අනුගමනය කරන්න, මිනිත්තු 5 කින් ඔබට ඔබේ වෙබ් අඩවියේ MathJax හි සියලුම විශේෂාංග භාවිතා කිරීමට හැකි වනු ඇත.

ප්‍රධාන MathJax වෙබ් අඩවියෙන් හෝ ලේඛන පිටුවෙන් ලබාගත් කේත විකල්ප දෙකක් භාවිතයෙන් ඔබට දුරස්ථ සේවාදායකයකින් MathJax පුස්තකාල ස්ක්‍රිප්ට් සම්බන්ධ කළ හැක:

මෙම කේත විකල්පයන්ගෙන් එකක් ඔබේ වෙබ් පිටුවේ කේතයට පිටපත් කර ඇලවිය යුතුය, වඩාත් සුදුසු වන්නේ ටැග් අතර සහ හෝ ටැගයට පසුව වහාම. පළමු විකල්පයට අනුව, MathJax වේගයෙන් පූරණය වන අතර පිටුව අඩුවෙන් මන්දගාමී වේ. නමුත් දෙවන විකල්පය මගින් MathJax හි නවතම අනුවාද ස්වයංක්‍රීයව නිරීක්ෂණය කර පූරණය කරයි. ඔබ පළමු කේතය ඇතුල් කරන්නේ නම්, එය වරින් වර යාවත්කාලීන කිරීමට අවශ්ය වනු ඇත. ඔබ දෙවන කේතය ඇතුළත් කළහොත්, පිටු වඩාත් සෙමින් පූරණය වනු ඇත, නමුත් ඔබට MathJax යාවත්කාලීනයන් නිරන්තරයෙන් නිරීක්ෂණය කිරීමට අවශ්‍ය නොවනු ඇත.

MathJax සම්බන්ධ කිරීමට පහසුම ක්‍රමය වන්නේ Blogger හෝ WordPress: අඩවි පාලන පැනලය තුළ, තුන්වන පාර්ශ්ව ජාවාස්ක්‍රිප්ට් කේතය ඇතුළු කිරීමට නිර්මාණය කර ඇති විජට් එකක් එක් කරන්න, ඉහත ඉදිරිපත් කර ඇති බාගැනීම් කේතයේ පළමු හෝ දෙවන අනුවාදය එයට පිටපත් කර විජට් එක සමීප කරන්න. අච්චුවේ ආරම්භයට (මාර්ගය වන විට, මෙය කිසිසේත්ම අවශ්‍ය නොවේ , MathJax ස්ක්‍රිප්ට් එක අසමමුහුර්තව පටවා ඇති බැවින්). එච්චරයි. දැන් MathML, LaTeX, සහ ASCIIMathML හි සලකුණු වාක්‍ය ඛණ්ඩය ඉගෙන ගන්න, ඔබ ඔබේ වෙබ් අඩවියේ වෙබ් පිටුවලට ගණිතමය සූත්‍ර ඇතුළු කිරීමට සූදානම්.

ඕනෑම ඛණ්ඩනය නිශ්චිත රීතියකට අනුව ගොඩනගා ඇති අතර එය අසීමිත වාර ගණනක් අඛණ්ඩව යොදනු ලැබේ. එවැනි සෑම වේලාවක්ම පුනරාවර්තනයක් ලෙස හැඳින්වේ.

මෙන්ගර් ස්පොන්ජියක් තැනීම සඳහා පුනරාවර්තන ඇල්ගොරිතම තරමක් සරල ය: 1 පැත්ත සහිත මුල් ඝනකයක් එහි මුහුණුවලට සමාන්තරව ගුවන් යානා මගින් සමාන ඝනක 27 කට බෙදා ඇත. එක් මධ්ය ඝනකයක් සහ මුහුණු දිගේ එයට යාබදව ඇති ඝනක 6 ක් එයින් ඉවත් කරනු ලැබේ. ප්රතිඵලය වන්නේ ඉතිරි කුඩා කැට 20 කින් සමන්විත කට්ටලයකි. මෙම එක් එක් ඝනකයක් සමඟම එසේ කිරීමෙන්, අපට කුඩා කැට 400 කින් සමන්විත කට්ටලයක් ලැබේ. මෙම ක්රියාවලිය නිමක් නැතිව දිගටම කරගෙන යාම, අපි මෙන්ගර් ස්පොන්ජියක් ලබා ගනිමු.

විකර්ණ න්‍යාස වලට සරලම ව්‍යුහය ඇත. රේඛීය ක්‍රියාකරුගේ න්‍යාසයට විකර්ණ ස්වරූපයක් ඇති පදනමක් සොයාගත හැකිද යන ප්‍රශ්නය පැන නගී. එවැනි පදනමක් පවතී.
අපට රේඛීය අවකාශයක් ලබා දෙමු R n සහ එහි ක්‍රියා කරන රේඛීය ක්‍රියාකරු A; මෙම අවස්ථාවෙහිදී, A ක්රියාකරු R n තමා තුළට ගනී, එනම් A:R n → R n .

අර්ථ දැක්වීම. ශුන්‍ය නොවන දෛශිකයක් A ක්‍රියාකරු A හි eigenvector ලෙස හැඳින්වේ නම්, A ක්‍රියාකරු එයට සම්බන්ධ දෛශිකයකට සිතියම්ගත කළහොත්, එනම්. λ අංකය eigenvactor ට අනුරූප වන A ක්‍රියාකරුගේ eigenvalue හෝ eigenvalue ලෙස හැඳින්වේ.
eigenvalues ​​සහ eigenvectors හි සමහර ගුණාංග අපි සටහන් කරමු.
1. අයිගන් දෛශිකවල ඕනෑම රේඛීය සංයෝජනයක් ක්‍රියාකරු A එකම eigenvalue λ ට අනුරූප වන eigenvactor එකකි.
2. Eigenvectors යුගල වශයෙන් වෙනස් eigenvalues ​​λ 1 , λ 2 , ..., λ m සමඟ ක්‍රියාකරු A රේඛීයව ස්වාධීන වේ.
3. eigenvalues ​​λ 1 =λ 2 = λ m = λ නම්, eigenvalue λ රේඛීයව ස්වාධීන අයිගන් දෛශික m ට වඩා අනුරූප නොවේ.

එබැවින්, n රේඛීය ස්වාධීන අයිගන් දෛශික තිබේ නම් , විවිධ eigenvalues ​​λ 1, λ 2, ..., λ n වලට අනුරූප වේ, එවිට ඒවා රේඛීයව ස්වාධීන වේ, එබැවින් ඒවා R n අවකාශයේ පදනම ලෙස ගත හැකිය. රේඛීය ක්‍රියාකරු A හි න්‍යාසයේ ස්වරූපය එහි අයිගන් දෛශිකවල පදනමින් සොයා ගනිමු, ඒ සඳහා අපි A පාදක දෛශික මත ක්‍රියා කරන්නෙමු: එතකොට .
මේ අනුව, එහි අයිගන් දෛශිකවල පදනම මත රේඛීය ක්‍රියාකරු A හි න්‍යාසයට විකර්ණ ස්වරූපයක් ඇති අතර A ක්‍රියාකරුගේ අයිගන් අගයන් විකර්ණය දිගේ ඇත.
අනුකෘතියට විකර්ණ ස්වරූපයක් ඇති තවත් පදනමක් තිබේද? මෙම ප්‍රශ්නයට පිළිතුර පහත ප්‍රමේය මගින් ලබා දේ.

ප්රමේයය. A පදනමේ (i = 1..n) රේඛීය ක්‍රියාකරුගේ න්‍යාසයට විකර්ණ ආකාරයක් ඇත, පදනමේ සියලුම දෛශික A ක්‍රියාකරුගේ අයිගන් දෛශික නම් සහ පමණි.

eigenvalues ​​සහ eigenvectors සෙවීමේ රීතිය දෛශිකයක් ලබා දෙමු , මෙහි x 1, x 2, ..., x n යනු පදනමට සාපේක්ෂව දෛශිකයේ ඛණ්ඩාංක වේ සහ eigenvalue λ ට අනුරූප වන රේඛීය ක්‍රියාකරු A හි eigenvector වේ, එනම්. මෙම සම්බන්ධතාවය matrix ආකාරයෙන් ලිවිය හැක

. (*)


සමීකරණය (*) සොයා ගැනීම සඳහා සමීකරණයක් ලෙස සැලකිය හැකි අතර, එනම්, අයිගන් දෛශිකය ශුන්‍ය විය නොහැකි බැවින් අපි සුළු නොවන විසඳුම් ගැන උනන්දු වෙමු. සමජාතීය රේඛීය සමීකරණ පද්ධතියක සුළු නොවන විසඳුම් පවතිනුයේ det(A - λE) = 0 නම් සහ පමණක් බව දන්නා කරුණකි. මේ අනුව, λ ක්‍රියාකරු A හි අයිගන් අගයක් වීමට නම් det(A - λE) අවශ්‍ය සහ ප්‍රමාණවත් වේ. ) = 0.
සමීකරණය (*) ඛණ්ඩාංක ආකාරයෙන් විස්තරාත්මකව ලියා ඇත්නම්, අපි රේඛීය සමජාතීය සමීකරණ පද්ධතියක් ලබා ගනිමු:

(1)
කොහෙද - රේඛීය ක්‍රියාකරු අනුකෘතිය.

පද්ධතිය (1) එහි නිර්ණායකය D ශුන්‍යයට සමාන නම් ශුන්‍ය නොවන ද්‍රාවණයක් ඇත


Eigenvalues ​​සෙවීම සඳහා අපට සමීකරණයක් ලැබුණි.
මෙම සමීකරණය ලාක්ෂණික සමීකරණය ලෙස හඳුන්වනු ලබන අතර, එහි වම් පැත්ත න්‍යාසයේ (ක්‍රියාකරු) A හි ලාක්ෂණික බහුපද ලෙස හැඳින්වේ. ලාක්ෂණික බහුපදයට සැබෑ මූලයන් නොමැති නම්, A න්‍යාසයට අයිගන් දෛශික නොමැති අතර විකර්ණ ස්වරූපයට අඩු කළ නොහැක.
λ 1, λ 2, ..., λ n ලාක්ෂණික සමීකරණයේ සැබෑ මූලයන් වන අතර ඒවා අතර ගුණාකාර තිබිය හැක. මෙම අගයන් පද්ධතියට (1) ආදේශ කිරීමෙන්, අපි අයිගන් දෛශික සොයා ගනිමු.

උදාහරණ 12. රේඛීය ක්‍රියාකරු A නීතියට අනුව R 3 හි ක්‍රියා කරයි, එහිදී x 1, x 2, .., x n යනු දෛශිකයේ ඛණ්ඩාංක වේ. , , . මෙම ක්‍රියාකරුගේ eigenvalues ​​සහ eigenvectors සොයන්න.
විසඳුම. අපි මෙම ක්‍රියාකරුගේ අනුකෘතිය ගොඩනඟමු:
.
අපි eigenvectors හි ඛණ්ඩාංක තීරණය කිරීම සඳහා පද්ධතියක් නිර්මාණය කරමු:

අපි ලාක්ෂණික සමීකරණයක් සාදා එය විසඳන්නෙමු:

.
λ 1,2 = -1, λ 3 = 3.
පද්ධතියට λ = -1 ආදේශ කිරීම, අපට ඇත්තේ:
හෝ
මොකද , එවිට පරායත්ත විචල්‍ය දෙකක් සහ එක් නිදහස් විචල්‍යයක් ඇත.
x 1 නිදහස් නොදන්නා එකක් වීමට ඉඩ දෙන්න අපි මෙම පද්ධතිය ඕනෑම ආකාරයකින් විසඳා මෙම පද්ධතියේ පොදු විසඳුම සොයා ගනිමු: මූලික විසඳුම් පද්ධතිය n - r = 3 - 2 = 1 සිට එක් විසඳුමකින් සමන්විත වේ.
eigenvalue λ = -1 ට අනුරූප අයිගන් දෛශික කුලකයට පෝරමය ඇත: , x 1 යනු ශුන්‍ය නොවන ඕනෑම සංඛ්‍යාවක් වේ. අපි මෙම කට්ටලයෙන් එක් දෛශිකයක් තෝරා ගනිමු, උදාහරණයක් ලෙස, x 1 = 1 දැමීම: .
ඒ හා සමානව තර්ක කිරීම, අපි eigenvalue λ = 3 ට අනුරූප අයිගන් දෛශිකය සොයා ගනිමු: .
R 3 අවකාශයේ, පදනම රේඛීයව ස්වාධීන දෛශික තුනකින් සමන්විත වේ, නමුත් අපට ලැබුණේ රේඛීය ස්වාධීන eigenvectors දෙකක් පමණි, R 3 හි පදනම සෑදිය නොහැක. එහි ප්‍රතිඵලයක් ලෙස, රේඛීය ක්‍රියාකරුගේ න්‍යාස A විකර්ණ ස්වරූපයට අඩු කළ නොහැක.

උදාහරණ 13. අනුකෘතියක් ලබා දී ඇත .
1. දෛශිකය බව ඔප්පු කරන්න න්‍යාස A හි අයිගන් දෛශිකයකි. මෙම අයිගන් දෛශිකයට අනුරූප අයිගන් අගය සොයන්න.
2. න්‍යාස A හි විකර්ණ ආකාරයක් ඇති පදනමක් සොයන්න.
විසඳුම.
1. නම්, එය අයිගන් දෛශිකයකි

.
දෛශිකය (1, 8, -1) යනු අයිගන් දෛශිකයකි. Eigenvalue λ = -1.
න්‍යාසයට අයිගන් දෛශික වලින් සමන්විත පදනමක විකර්ණ ස්වරූපයක් ඇත. ඔවුන්ගෙන් එක් කෙනෙක් ප්රසිද්ධයි. ඉතුරු ටික හොයාගමු.
අපි පද්ධතියෙන් eigenvectors සොයන්නෙමු:

ලාක්ෂණික සමීකරණය: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
λ = -3 eigenvalue ට අනුරූප අයිගන් දෛශිකය සොයා ගනිමු:

මෙම පද්ධතියේ න්‍යාසයේ ශ්‍රේණිය දෙකක් වන අතර නොදන්නා සංඛ්‍යාවට සමාන වේ, එබැවින් මෙම පද්ධතියට ඇත්තේ ශුන්‍ය ද්‍රාවණයක් පමණි 1. මේ අනුව, දෛශිකය (0 ,1,0) යනු λ = -3 ට අනුරූප වන අයිගන් දෛශිකයකි. අපි පරීක්ෂා කරමු:
.
λ = 1 නම්, අපි පද්ධතිය ලබා ගනිමු
අනුකෘතියේ ශ්‍රේණිය දෙකකි. අපි අවසාන සමීකරණය ඉක්මවා යනවා.
x 3 නොමිලේ නොදන්නා එකක් වේවා. එවිට x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
x 3 = 1 යැයි උපකල්පනය කළහොත්, අප සතුව (-3,-9,1) - eigenvalue λ = 1 ට අනුරූප වන අයිගන් දෛශිකයක් ඇත. පරීක්ෂා කරන්න:

.
අයිගන් අගයන් සැබෑ සහ වෙනස් බැවින් ඒවාට අනුරූප දෛශික රේඛීයව ස්වාධීන වන බැවින් ඒවා R 3 හි පදනම ලෙස ගත හැකිය. මේ අනුව, පදනම තුළ , , matrix A ආකෘතිය ඇත:
.
රේඛීය ක්‍රියාකරුගේ සෑම න්‍යාසයක්ම A:R n → R n විකර්ණ ආකාරය දක්වා අඩු කළ නොහැක, මන්ද සමහර රේඛීය ක්‍රියාකරුවන් සඳහා රේඛීය ස්වාධීන eigenvectors n ට වඩා අඩු විය හැක. කෙසේ වෙතත්, න්‍යාසය සමමිතික නම්, ගුණිත m හි ලාක්ෂණික සමීකරණයේ මූලය හරියටම m රේඛීය ස්වාධීන දෛශිකවලට අනුරූප වේ.

අර්ථ දැක්වීම. සමමිතික න්‍යාසයක් යනු ප්‍රධාන විකර්ණය පිළිබඳ සමමිතික මූලද්‍රව්‍ය සමාන වන හතරැස් න්‍යාසයකි, එනම් .
සටහන්. 1. සමමිතික න්‍යාසයක සියලුම eigenvalues ​​සැබෑ වේ.
2. යුගල වශයෙන් වෙනස් අයිගන් අගයන්ට අනුරූප වන සමමිතික න්‍යාසයක අයිගන් දෛශික විකලාංග වේ.
අධ්‍යයනය කරන ලද උපකරණයේ බොහෝ යෙදුම් වලින් එකක් ලෙස, දෙවන පෙළ වක්‍රයක වර්ගය තීරණය කිරීමේ ගැටලුව අපි සලකා බලමු.



ඔබ ලිපියට කැමතිද? එය හුවමාරු කරගන්න
මෙම ලිපිය මුද්‍රණය කරන්න
ඉහළ