Método de linealización armónica: Directrices para el trabajo de laboratorio. Linealización armónica Coeficientes de linealización armónica

Como ya se señaló, en los ASR no lineales y especialmente de retransmisión, oscilaciones periódicas estables amplitud y frecuencia constantes, las llamadas auto-oscilaciones. Además, las autooscilaciones pueden persistir incluso con cambios significativos en los parámetros del sistema. La práctica ha demostrado que en muchos casos las oscilaciones de la variable controlada (Fig. 3) son cercanas a las armónicas.

La proximidad de las autooscilaciones a las armónicas nos permite utilizar el método de linealización armónica para determinar sus parámetros: amplitud A y frecuencia w 0. El método se basa en el supuesto de que la parte lineal del sistema es un filtro de paso bajo (hipótesis del filtro). Determinemos las condiciones bajo las cuales las autooscilaciones en el sistema pueden ser cercanas a las armónicas. Limitémonos a sistemas que, como en la Fig. 3 se puede reducir a una conexión en serie de un elemento no lineal y una parte lineal. Supongamos que la señal de referencia es un valor constante, por simplicidad la tomaremos igual a cero; Y la señal de error (Figura 3) es armónica:

La señal de salida de un elemento no lineal, como cualquier señal periódica (en la Figura 3, son oscilaciones rectangulares), se puede representar como la suma de los armónicos de la serie de Fourier.

Supongamos que la parte lineal del sistema es un filtro de paso bajo (Fig. 4) y pasa solo el primer armónico con frecuencia w 0. Los segundos con una frecuencia de 2w 0 y los armónicos superiores son filtrados por la parte lineal. En este caso, sobre salida lineal las piezas existirán prácticamente sólo primer armónico , y la influencia de los armónicos superiores puede despreciarse

Por tanto, si la parte lineal del sistema es un filtro de paso bajo y la frecuencia de las autooscilaciones w 0 satisface las condiciones

, (4)

La suposición de que la parte lineal del sistema es un filtro de paso bajo se llama hipótesis de filtro . La hipótesis del filtro siempre se cumple si la diferencia en los grados de los polinomios del denominador y numerador de la función de transferencia de la parte lineal

al menos dos

La condición (6) se cumple para muchos sistemas reales. Un ejemplo es un enlace aperiódico de segundo orden y un integrador real.

Al estudiar las autooscilaciones cercanas a los armónicos, solo se tiene en cuenta el primer armónico de las oscilaciones periódicas en la salida de un elemento no lineal, ya que los armónicos más altos todavía son prácticamente filtrados por la parte lineal. En el modo de autooscilación, se realiza linealización armónica elemento no lineal. El elemento no lineal se reemplaza por uno lineal equivalente con ganancia compleja (función descriptiva) dependiendo de la amplitud de la señal armónica de entrada:

donde y son las partes real e imaginaria,

- argumento,

– módulo.

En el caso general, depende tanto de la amplitud como de la frecuencia de las autooscilaciones y del componente constante. Ganancia físicamente compleja de un elemento no lineal, más a menudo llamada coeficiente de linealización armónica , Hay ganancia compleja de un elemento no lineal en el primer armónico. Módulo del coeficiente de linealización armónica.

es numéricamente igual a la relación entre la amplitud del primer armónico en la salida del elemento no lineal y la amplitud de la señal armónica de entrada.

Argumento

caracteriza el cambio de fase entre el primer armónico de las oscilaciones de salida y la señal armónica de entrada. Para no linealidades inequívocas, como, por ejemplo, en la Fig. 2,a y 2,b, expresión real y

Para no linealidades ambiguas, la Fig. 2,c, 2,d, determinado por la fórmula

donde S es el área del bucle de histéresis. El área S se toma con un signo más si el circuito de histéresis se deriva en dirección positiva (Fig. 2, c) y con un signo menos en caso contrario (Fig. 2, d).

En el caso general y se calculan mediante las fórmulas.

donde , es una función no lineal (característica de un elemento no lineal).

Teniendo en cuenta lo anterior, al estudiar autooscilaciones cercanas a las armónicas, el ASR no lineal (Fig. 3) se reemplaza por uno equivalente con un coeficiente de linealización armónico en lugar de un elemento no lineal (Fig. 5). La señal de salida del elemento no lineal de la Fig. 5 se designa como , esto es

Destaca que un elemento no lineal sólo genera

el primer armónico de las oscilaciones. Las fórmulas para los coeficientes de linealización armónica para no linealidades típicas se pueden encontrar en la literatura, por ejemplo, en. En el Cuadro B del Apéndice se muestran las características de los elementos de relevo en estudio, fórmulas y sus hodógrafas. Fórmulas y hodógrafas para el coeficiente de linealización armónica inversa, definido por la expresión

donde están las partes real e imaginaria. Las hodógrafas y se construyen en coordenadas , y , respectivamente.

Anotemos ahora las condiciones para la existencia de autooscilaciones. El sistema de la Fig. 5 es equivalente a lineal. En un sistema lineal, existen oscilaciones no amortiguadas si está en el límite de estabilidad. Utilicemos la condición del límite de estabilidad según el criterio de Nyquist: . En la Fig. 6,a – dos puntos de intersección, lo que indica la presencia de dos ciclos límite.

Introducción

Los sistemas de relés se han generalizado en la práctica del control automático. La ventaja de los sistemas de relés es su simplicidad de diseño, confiabilidad, facilidad de mantenimiento y configuración. Los sistemas de relés representan una clase especial de sistemas de control automático no lineales.

A diferencia de los continuos en los sistemas de relés, la acción reguladora cambia abruptamente cada vez que la señal de control del relé (la mayoría de las veces es un error de control) pasa por algunos valores fijos (umbral), por ejemplo, por cero.

Los sistemas de relés, por regla general, tienen un alto rendimiento debido al hecho de que la acción de control en ellos cambia casi instantáneamente y el actuador está expuesto a una señal constante por partes de máxima amplitud. Al mismo tiempo, en los sistemas de relés se producen a menudo oscilaciones propias, lo que en muchos casos supone una desventaja. En este artículo se estudia un sistema de relés con cuatro leyes de control diferentes.

Estructura del sistema en estudio.

El sistema en estudio (Fig.) 1 incluye un elemento de comparación ES, un elemento de relé RE, un actuador (integrador ideal con ganancia = 1), un objeto de control (un enlace aperiódico con tres constantes de tiempo , y ganancia). Los valores de los parámetros del sistema se dan en la tabla. 1 Apéndice A.

Las características estáticas (características de entrada-salida) de los elementos del relé bajo estudio se muestran en la Fig. 2.

En la Fig. 2a muestra las características de un relé ideal de dos posiciones, en la Fig. 2b característica de un relé de tres posiciones con zona muerta. En la Fig. 2,c y 2,d muestran las características de un relé de dos posiciones con histéresis positiva y negativa, respectivamente.

El ASR investigado se puede modelar utilizando paquetes de modelado conocidos, por ejemplo SIAM o VisSim.

Comentario. En algunos paquetes de simulación, el valor de salida

la señal del relé solo puede tomar valores ±1 en lugar de ±B, donde B es un número arbitrario. En tales casos, es necesario tomar la ganancia del integrador igual a .

Orden de trabajo

Para completar el trabajo, cada alumno recibe una versión de los datos iniciales del profesor (ver sección 2).

El trabajo se realiza en dos etapas.

La primera etapa es computacional y de investigación (puede realizarse fuera del laboratorio).

La segunda etapa es experimental (realizada en el laboratorio). En esta etapa, utilizando uno de los paquetes, se simulan los procesos transitorios en el sistema en estudio para los modos calculados en la primera etapa y se verifica la precisión de los métodos teóricos.

El material teórico necesario se presenta en la sección 4; La sección 5 contiene preguntas de prueba.

3.1. Parte de cálculo e investigación.

1. Obtener expresiones para las características amplitud-frecuencia y fase-frecuencia, reales e imaginarias de la parte lineal del sistema.

2. Calcule y construya la característica de fase de amplitud de la parte lineal del sistema. Para los cálculos, utilice programas del paquete TAU. Necesariamente imprimir valores de respuesta de frecuencia reales e imaginarios(10 – 15 puntos correspondientes tercero y segundo cuadrantes).

4. Utilizando el método analítico gráfico de Goldfarb, determine la amplitud y frecuencia de las autooscilaciones y su estabilidad para los cuatro relés. Los parámetros de las autooscilaciones también se pueden calcular analíticamente. Representar cualitativamente el retrato de fase del sistema para cada caso.

5. Para un relé de tres posiciones, determine un valor de la ganancia de la parte lineal en el que no hay autooscilaciones y el valor límite en el que fallan las autooscilaciones.

parte experimental

1. Utilizando uno de los paquetes de modelado disponibles, cree un esquema de modelado para el ASR en estudio. Con el permiso del profesor, puedes utilizar un diagrama ya preparado. Configure los parámetros del circuito de acuerdo con la tarea.

2. Investigar el proceso transitorio en un sistema con un relé ideal (imprimir), aplicando una acción paso a paso x(t)=40*1(t) a la entrada. Mida la amplitud y frecuencia de las autooscilaciones, comparándolas con los valores calculados. Repita el experimento, estableciendo condiciones iniciales distintas de cero (por ejemplo, y(0)=10, y(1)(0)=-5).

3. Investigue el proceso transitorio en un sistema con un relé de tres posiciones para dos valores diferentes de la amplitud de la señal de entrada x(t)= 40*1(t) y x(t)=15*1(t). Imprima procesos transitorios, mida la amplitud y frecuencia de las autooscilaciones (si existen), compárelas con los valores calculados y saque conclusiones.

4. Investigar procesos transitorios en un sistema con relé de tres posiciones para otros valores de ganancia de la parte lineal (ver párrafo 5, sección 3.1).

5. Investigar procesos transitorios en un sistema con relés de dos posiciones con histéresis en condiciones iniciales cero y distintas de cero y x(t)=40*1(t). Imprima procesos transitorios, mida la amplitud y frecuencia de las autooscilaciones (si existen), compárelas con los valores calculados y saque conclusiones.

parte teorica

Un método ampliamente utilizado para calcular sistemas no lineales es el método de linealización armónica (descripción de funciones).

El método permite determinar los parámetros de las autooscilaciones (amplitud y frecuencia), la estabilidad de las autooscilaciones y la estabilidad de la posición de equilibrio de un ASR no lineal. Sobre la base del método de linealización armónica, se han desarrollado métodos para construir procesos transitorios, análisis y síntesis de ASR no lineales.

Método de linealización armónica

(1)

Por tanto, si la parte lineal del sistema es un filtro de paso bajo y la frecuencia de las autooscilaciones w 0 satisface las condiciones

, (4)

(5)

al menos dos

La condición (6) se cumple para muchos sistemas reales. Un ejemplo es un enlace aperiódico de segundo orden y un integrador real.

. (7)

donde y son las partes real e imaginaria,

- argumento,

– módulo.

(9)

es numéricamente igual a la relación entre la amplitud del primer armónico en la salida del elemento no lineal y la amplitud de la señal armónica de entrada.

Argumento

(10)

Para no linealidades ambiguas, la Fig. 2,c, 2,d, determinado por la fórmula

En el caso general y se calculan mediante las fórmulas.

, (12)

donde , es una función no lineal (característica de un elemento no lineal).

enfatiza que el elemento no lineal genera solo

, (13)

donde están las partes real e imaginaria. Las hodógrafas y se construyen en coordenadas , y , respectivamente.

. (14)

Ecuación (14) Hay condición para la existencia de autooscilaciones, cercano a lo armónico. Si hay muy positivo soluciones A y w 0 de la ecuación (14), entonces en el ASR no lineal hay autooscilaciones cercanas a las armónicas. De lo contrario, las autooscilaciones están ausentes o no son armónicas. La ecuación (14) se divide en dos – con respecto a las partes real e imaginaria:

;

Dividiendo ambos lados de la ecuación (14) por y teniendo en cuenta la fórmula (13), obtenemos la condición para la existencia de autooscilaciones en la forma de L.S.

. (17)

La ecuación (17) también se divide en dos:

(18)

y en algunos casos es más conveniente utilizarlos para determinar los parámetros de las autooscilaciones.

Goldfarb propuso un método gráfico-analítico para resolver el sistema (17) y determinar la estabilidad de las autooscilaciones.

En coordenadas , y , hodógrafas y se construyen (Fig. 6, a). Si las hodógrafas se cruzan, entonces existen autooscilaciones. Los parámetros de las autooscilaciones - A y w 0 se determinan en los puntos de intersección - frecuencia w 0 según la hodógrafa, amplitud según la hodógrafa. En la Fig. 6,a – dos puntos de intersección, lo que indica la presencia de dos ciclos límite.

Para determinar la estabilidad de las autooscilaciones, según Goldfarb, el lado izquierdo del AFC de la parte lineal se sombrea cuando se mueve a lo largo del AFC en la dirección de aumento de frecuencia (Fig. 6).

Las autooscilaciones son estables si, en el punto de intersección, la hodógrafa de un elemento no lineal pasa del área no sombreada al área sombreada cuando se mueve en la dirección de amplitud creciente A.

Si la transición se produce de un área sombreada a un área no sombreada, entonces las autooscilaciones no son estables.

En la Fig. La Figura 6b representa cualitativamente el retrato de fase correspondiente a dos ciclos límite en la Fig. 6, a. El punto de intersección con los parámetros y en la Fig. 6a corresponde al ciclo límite inestable en la Fig. 6b, punto con parámetros y y para lograr la interrupción de las autooscilaciones, en este caso hodógrafas y no se cruzan. Se puede lograr el mismo efecto aumentando la zona muerta d o reduciendo la amplitud de la señal de salida del relé B. Existe un cierto valor límite K l en el que el AFC de la parte lineal toca ¡Error! Error de comunicación. donde , y el valor de amplitud es . Naturalmente, esto conduce a un cambio cualitativo en el retrato de fases del sistema.

Linealización armónica de elementos no lineales. Este método se utiliza para estudiar sistemas no lineales con una parte lineal superior al tercer orden. En la mayoría de los sistemas, el proceso transitorio es una oscilación amortiguada, por lo tanto, en la entrada del elemento no lineal, se transmite una señal periódica con una amplitud que varía lentamente a través del circuito de retroalimentación principal (GOS) y, en presencia de una señal de entrada, junto con un componente constante.

Supondremos que a la entrada del elemento no lineal durante un pequeño período de tiempo inicial la amplitud y la frecuencia no cambian o corresponden a la amplitud y frecuencia de las autooscilaciones del sistema. A la salida del NE obtenemos una función periódica que se puede expandir a una serie de Fourier. Cuando se estudian sistemas no lineales, la mayoría de las veces solo se utiliza el primer componente armónico, porque En la mayoría de los casos, la parte lineal del sistema es un filtro de paso bajo. Pero para comprobar esto y la aplicabilidad de este método de investigación, es necesario determinar la frecuencia de las autooscilaciones en el sistema, a partir de lo cual podemos determinar posteriormente la capacidad de la parte lineal para filtrar armónicos superiores. Para ello se construye la respuesta en frecuencia de la parte lineal (LP).

Sea el sistema LF un filtro de paso bajo y asumiremos que las oscilaciones en la entrada del elemento NE no lineal son sinusoidales, entonces la señal de salida del NE es:

Dónde un a Y VC– Coeficientes de expansión de Fourier de la función no lineal:

Si la característica no lineal es simétrica y neutra, entonces el coeficiente de expansión de la serie de Fourier VC=0 y no hay armónicos pares en la expansión:

Usando estas relaciones, expresamos el valor del seno y el coseno en términos de la señal de entrada.

Sustituyamos estas relaciones en la ecuación de la salida NE y tengamos en cuenta sólo el primer armónico.

Escribamos esta ecuación en forma de operador:

Coeficiente A 0 – amplitud de las autooscilaciones; q es el coeficiente de linealización armónica para la componente sinusoidal, depende de la amplitud de la señal en la entrada NE; b 1 – coeficiente de linealización armónica para el componente coseno; ω 0 – amplitud de las autooscilaciones.

En ausencia de una componente constante en la entrada del NE, obtenemos una ecuación para describir el comportamiento del NE:

Esta es la ecuación de linealización armónica de NE.

Un NE armónicamente linealizado se puede representar como:

En este caso, podemos derivar la función de transferencia para el EN:

en ausencia de un componente constante en la entrada.

Coeficiente A 0 – amplitud de las autooscilaciones;

q es el coeficiente de linealización armónica para la componente sinusoidal, depende de la amplitud de la señal en la entrada del NE;

b 1 – coeficiente de linealización armónica para el componente coseno;

ω 0 – amplitud de las autooscilaciones.

La parte lineal del sistema se ve afectada por la señal de salida del NE, que contiene todo el espectro de frecuencias de la expansión de Fourier. Debido al principio de superposición, podemos suponer que cada armónico actúa sobre la parte lineal independientemente del otro. Por tanto, se pueden establecer oscilaciones periódicas a la salida del sistema, las cuales contendrán todo el espectro de frecuencias correspondientes a la señal NE, pero la amplitud de cada armónico estará determinada por el coeficiente de conversión del lado derecho del armónico considerado ( ).

Al sustituir la respuesta de frecuencia de la parte lineal, puede establecer la relación del cambio en amplitudes para cada armónico y verificar si la parte lineal es un filtro de paso bajo (si se pueden descartar los armónicos más altos).

Si se establece la frecuencia de las autooscilaciones y se conocen los coeficientes de linealización armónica del NE, teniendo en cuenta solo el primer armónico, entonces la frecuencia (frecuencia del primer armónico). Si es así, se pueden descartar armónicos más altos y este método es adecuado. Aquellos. podemos limitarnos a calcular un solo armónico en la salida NE. Entonces, para una característica impar única, el NE tendrá:

Para característica impar de histéresis:

En el primer caso, el NE equivale a un enlace libre de inercia con algunas características: el coeficiente de proporcionalidad depende de la amplitud o frecuencia de la señal en la entrada del NE.

En el caso de no linealidad histerética, el vínculo es equivalente al vínculo forzado. La peculiaridad de este método de linealización permite el uso de métodos frecuenciales de la teoría lineal para analizar un sistema no lineal.

Ministerio de Educación y Ciencia de la Federación de Rusia

Universidad Técnica Estatal de Saratov

Instituto Balakovo de Ingeniería, Tecnología y Gestión

Método de linealización armónica

Lineamientos para el trabajo de laboratorio en la asignatura “Teoría del Control Automático” para estudiantes de la especialidad 210100

Aprobado

consejo editorial y editorial

Instituto de Tecnología de Balakovo,

tecnología y gestión

Balakovo 2004

Objeto del trabajo: Estudio de sistemas no lineales utilizando el método de linealización armónica (equilibrio armónico), determinación de coeficientes de linealización armónica para varios enlaces no lineales. Adquirir habilidades para encontrar los parámetros de oscilaciones simétricas de amplitud y frecuencia constantes (autooscilaciones), utilizando métodos algebraicos, de frecuencia y también utilizando el criterio de Mikhailov.

INFORMACIÓN BÁSICA

El método de linealización armónica se refiere a métodos aproximados para estudiar sistemas no lineales. Permite evaluar de forma bastante sencilla y con una precisión aceptable la estabilidad de sistemas no lineales y determinar la frecuencia y amplitud de las oscilaciones establecidas en el sistema.

Se supone que el SCA no lineal en estudio se puede representar de la siguiente forma

y la parte no lineal debe tener una no linealidad

. (1)

Esta no linealidad puede ser continua o de retransmisión, de un solo valor o histerética.

Cualquier función o señal se puede expandir en una serie según un sistema de funciones linealmente independientes, en un caso particular, ortonormales. La serie de Fourier se puede utilizar como serie ortogonal.

Ampliemos la señal de salida de la parte no lineal del sistema en una serie de Fourier.

, (2)

aquí están los coeficientes de Fourier,

. (3)

Por tanto, la señal según (2) se puede representar como una suma infinita de armónicos con frecuencias crecientes. etc. Esta señal se suministra a la entrada de la parte lineal del sistema no lineal.

Denotemos la función de transferencia de la parte lineal.

, (4)

y el grado del polinomio del numerador debe ser menor que el grado del polinomio del denominador. En este caso, la respuesta de frecuencia de la parte lineal tiene la forma

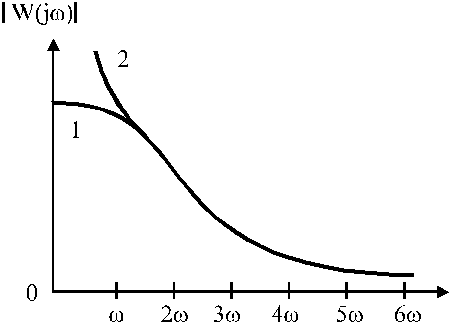
donde 1 - no tiene polos, 2 - tiene un polo o polos.

Para la respuesta de frecuencia es justo escribir

Por tanto, la parte lineal de un sistema no lineal es un filtro de paso alto. En este caso, la parte lineal transmitirá solo frecuencias bajas sin atenuación, mientras que las frecuencias altas se atenuarán significativamente a medida que aumente la frecuencia.

En el método de linealización armónica, se supone que la parte lineal del sistema pasará solo por el componente CC de la señal y el primer armónico. Entonces la señal en la salida de la parte lineal tendrá la forma

Esta señal pasa por todo el circuito cerrado del sistema Fig. 1 y a la salida del elemento no lineal sin tener en cuenta armónicos superiores, según (2) tenemos

. (7)

Al estudiar sistemas no lineales utilizando el método de linealización armónica, son posibles casos de oscilaciones simétricas y asimétricas. Consideremos el caso de oscilaciones simétricas. Aquí y.

Introduzcamos la siguiente notación.

Sustituyéndolos en (7), obtenemos. (8)

Teniendo en cuenta que

, Dónde ,

. (9)

Según (3) y (8) cuando

. (10)

La expresión (9) es la linealización armónica de la no linealidad. establece una relación lineal entre la variable de entrada y la variable de salida en . Las cantidades y se denominan coeficientes de linealización armónica.

Cabe señalar que la ecuación (9) es lineal para cantidades específicas y (la amplitud y frecuencia de las oscilaciones armónicas en el sistema). Pero en general conserva propiedades no lineales, ya que los coeficientes son diferentes para diferentes y . Esta característica nos permite estudiar las propiedades de sistemas no lineales utilizando el método de linealización armónica [Popov E.P.].

En el caso de oscilaciones asimétricas, la linealización armónica de la no linealidad conduce a la ecuación lineal

. (12)

Al igual que la ecuación (9), la ecuación linealizada (11) conserva las propiedades de un elemento no lineal, ya que los coeficientes de linealización armónica, así como la componente constante dependen tanto del desplazamiento como de la amplitud de las oscilaciones armónicas.

Las ecuaciones (9) y (11) nos permiten obtener las funciones de transferencia de elementos no lineales armónicamente linealizados. Entonces para vibraciones simétricas

Cuando se aplica una señal armónica a la entrada de un sistema lineal

También se establece una señal armónica en la salida del sistema, pero con una amplitud y un desplazamiento de fase diferentes con respecto a la entrada. Si se aplica una señal sinusoidal a la entrada de un elemento no lineal, entonces se forman oscilaciones periódicas en su salida, pero su forma es significativamente diferente de las sinusoidales. Como ejemplo en la Fig. La Figura 8.17 muestra la naturaleza del cambio en la variable de salida de un elemento no lineal con una característica de relé (8.14) cuando llegan oscilaciones sinusoidales (8.18) a su entrada.

Al expandir la señal periódica en la salida de un elemento no lineal a una serie de Fourier, la representamos como la suma de un componente constante y un número infinito de componentes armónicos:

, (8.19)

Dónde – coeficientes constantes de la serie de Fourier; – frecuencia de oscilaciones del primer armónico (frecuencia fundamental), igual a la frecuencia de oscilaciones sinusoidales de entrada; T- el período de oscilación del primer armónico, igual al período de las oscilaciones sinusoidales de entrada.

La señal de salida del elemento no lineal se alimenta a la entrada de la parte lineal del ACS (ver Fig. 8.1), que, por regla general, tiene una inercia significativa. En este caso, los componentes de alta frecuencia de la señal (8.19) prácticamente no pasan a la salida del sistema, es decir, la parte lineal es un filtro en relación con los componentes armónicos de alta frecuencia. En este sentido, y teniendo en cuenta también que las amplitudes de los componentes armónicos disminuyen al aumentar la frecuencia armónica, para una estimación aproximada del valor de salida de un elemento no lineal, en un gran número de casos basta con tener en cuenta sólo el primer componente armónico en.

En consecuencia, en ausencia de una componente constante en las oscilaciones de salida, la expresión (8.19) puede escribirse aproximadamente como:

Expresando la función de la fórmula (8.20) y de la derivada - función , transformamos la expresión (8.20) de la siguiente manera:

. (8.21)

Por tanto, la dependencia no lineal de la cantidad de salida de la cantidad de entrada en un elemento no lineal se reemplaza aproximadamente por una dependencia lineal descrita por la expresión (8.21).

Realizada la transformada de Laplace en la expresión (8.21), obtenemos:

En cuanto a los enlaces continuos, introducimos en consideración función de transferencia de un elemento no lineal linealizado armónicamente , como la relación entre la imagen de la cantidad de salida y la imagen de la cantidad de entrada:

. (8.22)

Tabla 8.1

Coeficientes de linealización armónica para no linealidades típicas.

Característica estática de un elemento no lineal.
Característica lineal con banda muerta.
Característica lineal con limitación.
Característica lineal con banda muerta y limitación.
Característica de reacción
Característica ideal del relé
Característica inequívoca del relé con banda muerta
Característica de relé ambigua con zona muerta.
Parábola cúbica:
Característica "bucle de histéresis"

La función de transferencia de un elemento no lineal tiene una diferencia significativa con la función de transferencia de un sistema lineal en que depende de la amplitud y frecuencia de la señal de entrada.

Escribimos la expresión (8.22) en la forma:

q(A) + q 1 (A), (8.23)

Dónde q(A),q 1 (A)– coeficientes de linealización armónica, definidos como la relación entre los coeficientes de la serie de Fourier para el primer armónico de las oscilaciones de salida y la amplitud de las oscilaciones de entrada:

q(A) = q 1 (A) = . (8.24)

Reemplazo en expresión (8.23) R en , obtenemos una expresión para coeficiente de transmisión complejo de un elemento no lineal :

q(A) +j q 1 (A), (8.25)

que es un análogo del AFC para un enlace lineal.

Como ejemplo, definamos una expresión para el coeficiente de transmisión complejo de un elemento no lineal con una característica estática de relé (8.14). Coeficientes de la serie de Fourier A 1 Y B 1 para la no linealidad especificada son iguales a:

B 1 .

Obviamente, el coeficiente B 1 será igual a cero para cualquier elemento no lineal con no linealidad estática simétrica impar.

Dónde - función de transferencia de la parte lineal del sistema; - Función de transferencia de un elemento no lineal después de su linealización.

Si , entonces la expresión (8.26) se puede escribir como:

Reemplazo en expresión (8.27) R En , obtenemos una expresión compleja en la que es necesario distinguir las partes real e imaginaria:

[ q(A) +j q 1 (A) ] . (8.28)

En este caso, escribimos la condición para que ocurran oscilaciones periódicas en un sistema con frecuencia y amplitud:

(8.29)

Si las soluciones del sistema (8.29) son complejas o negativas, el régimen de autooscilaciones del sistema es imposible. La presencia de soluciones reales positivas para e indica la presencia de autooscilaciones en el sistema, cuya estabilidad debe verificarse.

Como ejemplo, encontraremos las condiciones para la aparición de autooscilaciones en un sistema de control automático si la función de transferencia de su parte lineal es igual a:

(8.30)

y un elemento no lineal del tipo “bucle de histéresis”.

La función de transferencia de un elemento no lineal armónicamente linealizado (ver Tabla 8.1) tiene la forma:

. (8.31)

Sustituyendo las expresiones (8.30) y (8.31) en la expresión (8.26) y reemplazando R en , encuentre una expresión para:

De aquí, de acuerdo con la expresión (8.29), obtenemos las siguientes condiciones para la ocurrencia de autooscilaciones en el sistema:

Resolver el sistema de ecuaciones (8.29) suele ser difícil, ya que los coeficientes de linealización armónica tienen una dependencia compleja de la amplitud de la señal de entrada. Además, además de determinar la amplitud y la frecuencia, es necesario evaluar la estabilidad de las autooscilaciones en el sistema.

Las condiciones para la aparición de autooscilaciones en un sistema no lineal y los parámetros de los ciclos límite se pueden estudiar utilizando criterios de estabilidad de frecuencia, por ejemplo, el criterio de estabilidad de Nyquist. Según este criterio, en presencia de autooscilaciones, la característica de fase de amplitud de un sistema armónicamente linealizado de bucle abierto es igual a

pasa por el punto (-1, j0). Por lo tanto, para y se cumple la siguiente igualdad:

. (8.32)

La solución a la ecuación (8.32) respecto a la frecuencia y amplitud de las autooscilaciones se puede obtener gráficamente. Para hacer esto, en el plano complejo es necesario, cambiando la frecuencia de 0 a , construir una hodógrafa del AFC de la parte lineal del sistema y, cambiando la amplitud A de 0 a , construya una hodógrafa de la característica inversa de la parte no lineal, tomada con signo menos. Si estas hodógrafas no se cruzan, entonces el modo de autooscilación no existe en el sistema en estudio (figura 8.18, b).

Cuando las hodógrafas se cruzan (figura 8.18, a), surgen autooscilaciones en el sistema, cuya frecuencia y amplitud están determinadas por los valores de y en el punto de intersección.

Si y - se cruzan en varios puntos (Fig. 8.18, a), esto indica la presencia de varios ciclos límite en el sistema. En este caso, las oscilaciones en el sistema pueden ser estables e inestables.

La estabilidad del modo autooscilador se evalúa de la siguiente manera. El modo de autooscilación es estable si el punto en la hodógrafa de la parte no lineal, correspondiente a una amplitud mayor que el valor en el punto de intersección de las hodógrafas, no está cubierto por la hodógrafa de la respuesta en frecuencia de la parte lineal de el sistema. De lo contrario, el modo autooscilador es inestable.

En la Fig. 8.18, y las hodógrafas se cruzan en los puntos 1 y 2. Punto 1 determina el modo inestable de las autooscilaciones, ya que el punto de la hodógrafa correspondiente al aumento de amplitud está cubierto por la hodógrafa de la respuesta de frecuencia de la parte lineal del sistema. El punto 2 corresponde a un modo estable de autooscilaciones, cuya amplitud está determinada por la hodógrafa y la frecuencia, por la hodógrafa.

Como ejemplo, evalúemos la estabilidad de las autooscilaciones en dos sistemas no lineales. Supondremos que las funciones de transferencia de las partes lineales de estos sistemas coinciden y son iguales:

pero los elementos no lineales incluidos en ellos son diferentes. Supongamos que el primer sistema incluya un elemento no lineal "relé ideal", descrito por el sistema (8.14), y que el segundo sistema incluya un elemento no lineal con una característica estática "parábola cúbica". Usando los datos de la Tabla 8.1, obtenemos:

En la Fig. 8.19 muestra las hodógrafas de estos sistemas junto con la hodógrafa del AFC de la parte lineal del sistema. Con base en lo anterior, se puede argumentar que en el primer sistema surgen auto-oscilaciones estables con frecuencia y amplitud, y en el segundo sistema las auto-oscilaciones son inestables.

¿Te gustó el artículo? Compártelo

Imprime este artículo